Mouse human alignment of transcriptomic signatures

Last updated on 2024-10-25 | Edit this page

Estimated time: 100 minutes

Overview

Questions

How do we perform a cross-species comparison?
Which aspects of disease does a model capture?

Objectives

Approaches to align mouse data to human data
Understand the human AD co-expression modules
Perform correlation analysis
Understand the biological domains of Alzheimer’s disease
Use biological domain annotations to compare between species

Author Gregory Cary, Jackson Laboratory

Aligning Human and Mouse Phenotype

Alzheimer’s Disease (AD) is complex, and we can not expect any animal model to fully recapitulate all aspects of late onset AD (LOAD) pathology. To study AD with animal models we must find dimensions through which we can align phenotypes between the models and human cohorts. In MODEL-AD we use the following data modalities to identify commonalities between mouse models and human cohorts:

Imaging (i.e. MRI and PET) to correspond with human imaging studies (e.g. ADNI)
Neuropathological phenotypes
Lots of ’omics — genomics, proteomics, and metabolomics

The ’omics comparisons allow for a much richer contrast, since a significant portion of genes are shared between these two species. Homology at the anatomical and neuropathological levels is less clear.

Overview of Human cohort data

The Accelerating Medicines Partnership-Alzheimer’s Disease Consortium (AMP-AD) has generated extensive sets of ’omics data from a variety of human Alzheimer’s disease cohorts. AMP-AD researchers are applying systems biology approaches toward the goal of elucidating AD mechanisms and highlighting potential therapeutic targets.

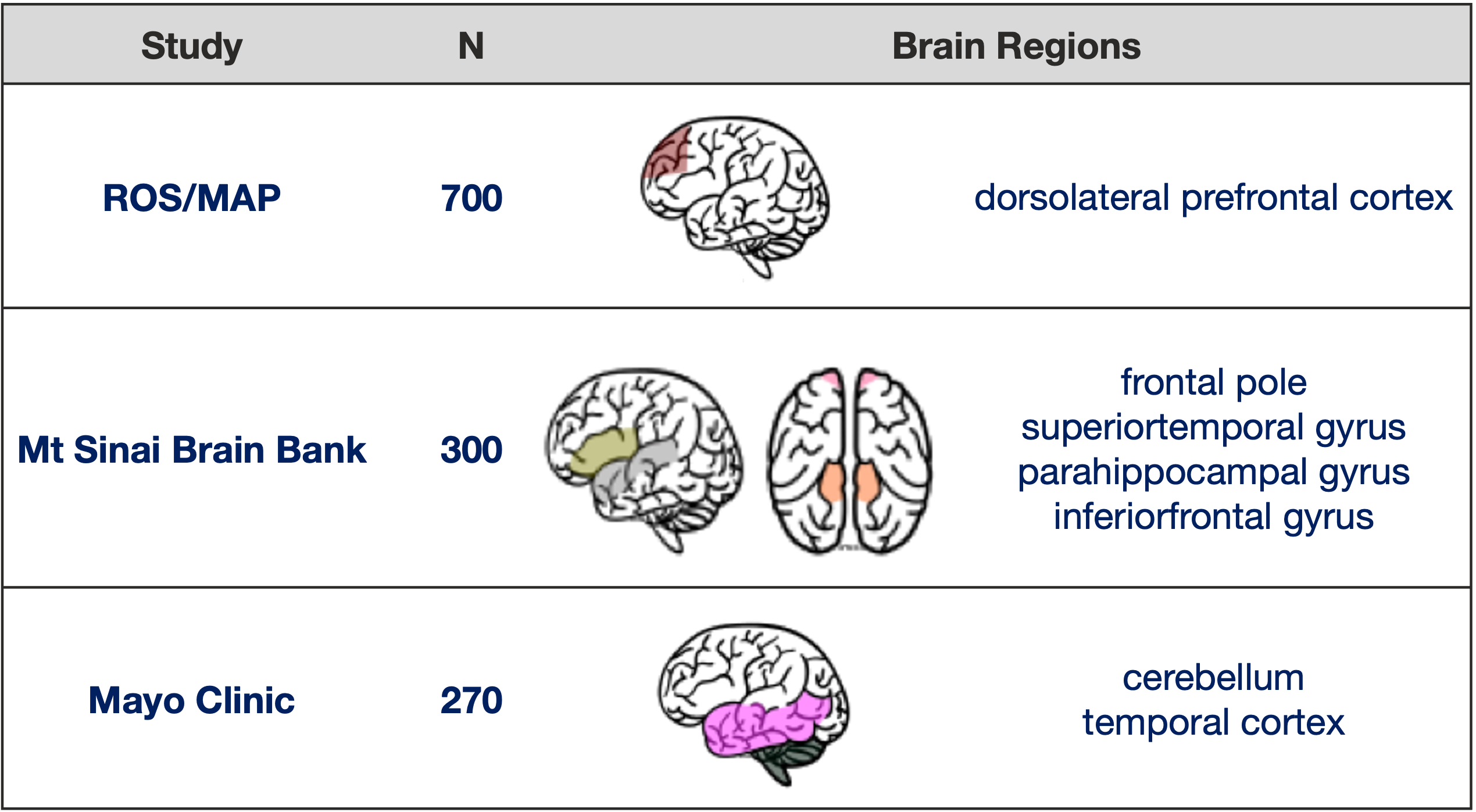
There are three large, independent human cohorts that are part of AMP-AD:

The Religious Orders Study and the Memory and Aging Project (ROSMAP, syn3219045)
Mount Sinai Brain Bank (MSBB, syn3159438)
Mayo Clinic (Mayo, syn5550404)

These studies have collected postmortem RNA-seq profiles from over 1,200 individuals spanning seven distinct brain regions: - dorsolateral prefrontal cortex (DLPFC)
- temporal cortex (TCX)
- inferior frontal gyrus (IFG)
- superior temporal gyrus (STG)
- frontal pole (FP)
- parahippocampal gyrus (PHG)
- cerebellum (CBE)

These samples are generally balanced for AD, MCI, and non-affected controls. The data provide a broad assessment on how AD affects multiple brain regions in 3 different populations in the US.

Transcriptomic studies of Alzheimer’s Disease

Today we’ll consider two different approaches to compare gene expression between human cohorts and model systems:

Correlation within co-expression module genes

correlations will be generally weak for all expression, but animal models may recapitulate specific aspects of the disease
we can use subsets of genes from co-expression modules, which represent genes expressed in similar patterns in AD, and look for correlations within these subsets

Correlation of functional enrichment results

another approach is to consider the functional annotation enriched among differentially expressed genes in human and mouse
we can similarly sub-divide these groups of co-functional genes into biological domains to aid our interpretation

Overview of Human Consensus RNA-Seq Coexpression Modules

Wan, et al. performed meta analysis including all available AMP-AD RNA-seq datasets and systematically defined correspondences between gene expression changes associated with AD in human brains. Briefly, the RNA-seq read libraries were normalized and covariates were adjusted for each human study separately before testing for differential expression using fixed/mixed effects modeling to account for batch effects. The expression data from each brain region was used to perform co-expression analysis using a variety of different algorithms, generating in total 2,978 co-expression modules across all tissues. Of these, 660 modules showed enrichment for at least one AD-specific differentially expressed gene from the meta-analysis of all cases compared to controls.

Wan et al clustered these modules together using network analyses and found 30 co-expression modules related to LOAD pathology. Among the 30 aggregate co-expression modules, five consensus clusters were described that span brain region and study cohorts. These consensus clusters consist of subsets of modules which are associated with similar AD related changes across brain regions and cohorts. Wan et al looked for enrichment of cell -type signatures within the modules using expression-weighted cell type enrichment analysis (Skene and Grant, 2016) and examined enrichment of functional annotations within the modules.

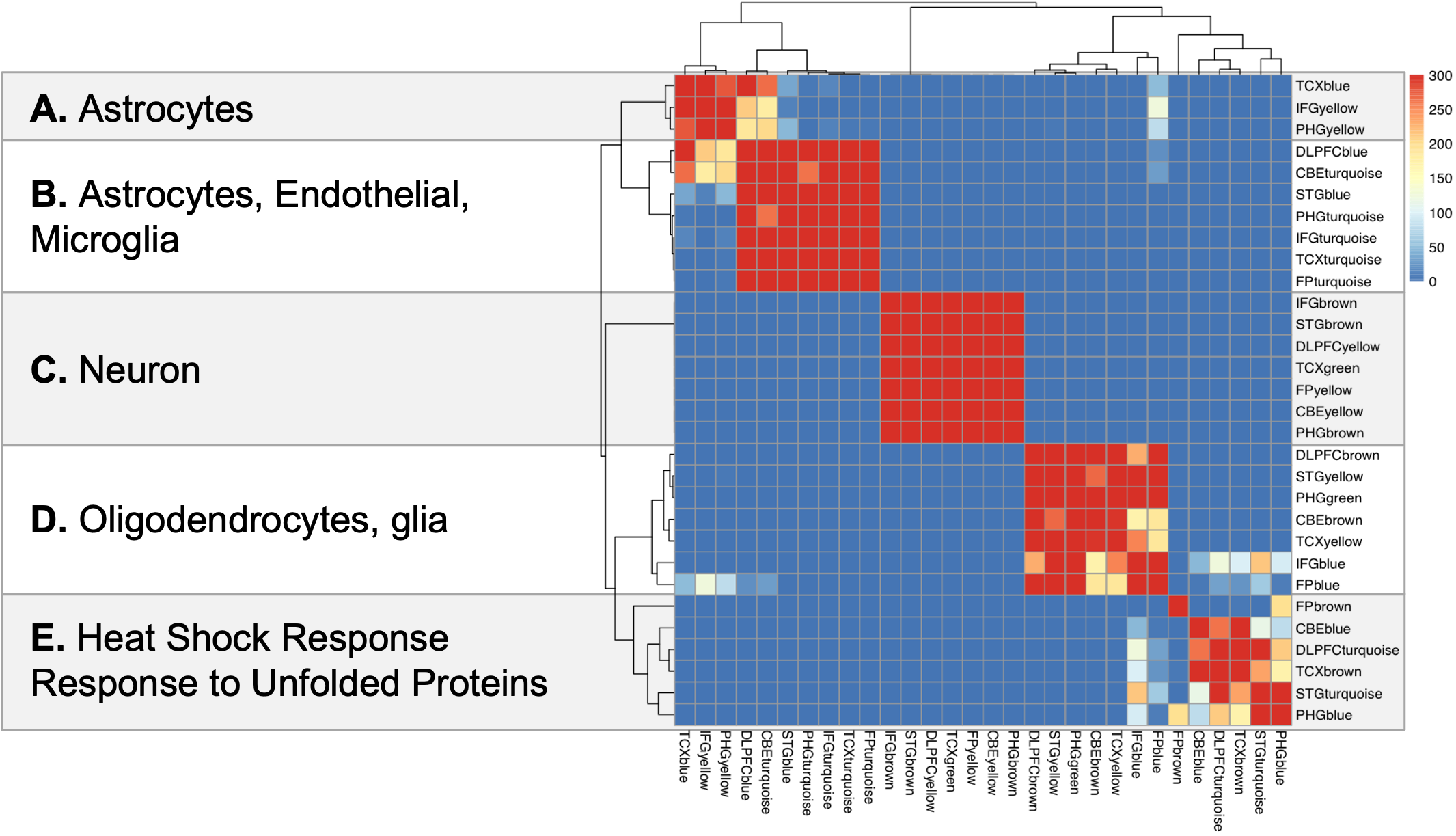
This figure shows a matrix view of gene content overlap between the 30 co-expression modules. You’ll note a few strongly overlapping group of modules, implicating similar expression profiles in different studies and brain regions, which are the consensus clusters (A-E).

The first module block (consensus cluster A) is enriched for signatures of astrocytes, while the next block (consensus cluster B) is enriched for signatures of other cell types, including endothelial and microglial expressed genes, suggesting an inflammation component. The third module block (consensus cluster C) is strongly enriched for signatures of neuronal gene expression, linking the modules within this cluster to neurodegenerative processes. The fourth module block (consensus cluster D) is enriched for oligodendrocyte and other glial genes, indicating myelination and other neuronal support functions associated with these modules. Finally, consensus cluster E contains mixed modules that don’t have clear cell type enrichments, but do have enrichments for processes involved in response to stress or unfolded proteins. Stress response is not cell specific, so the expression represented by these modules may be throughout many cells in the brain.

Accessing AMP-AD module data

These AMP-AD co-expression modules are very useful for making comparisons between animal models and the human cohorts. In order to use these modules to make the comparisons, we’ll need to download data pertaining to the 30 co-expression modules. These data are available from the Synapse data repository; let’s download and take a closer look at the data.

R

query <- synTableQuery("SELECT * FROM syn11932957")
module_table <- read.table(query$filepath, sep = ",",header = TRUE)

Let’s look at module table

R

head(module_table)

Here you see 9 columns in this table. Columns we’re interested in are:

column 3: GeneID contains Ensembl gene IDs
column 4: Module is the module name in which gene is clustered
column 7: brainRegion is the tissue of the corresponding module
column 9: external_gene_name are gene symbols

How many unique modules are in the table?

R

length(unique(module_table$Module))

What are the names of the modules?

R

unique(module_table$Module)

How many genes are in each module?

R

table(module_table$Module)

We can visualize this as bar plot using ggplot2 package.

R

ggplot(module_table,aes(y=Module)) + 
  geom_bar() + 
  theme_bw()

Challenge 1

What are other ways to count genes in each module?

Show me the solution

R

dplyr::count(module_table, Module)

We can also check the total number of unique genes in the table

R

length(unique(module_table$GeneID))

Mouse orthologs of Human module genes

In the module table we’ve downloaded we have human ENSEMBL ids and human gene symbols. In order to compare between human and mouse models, we will need to identify the corresponding mouse gene IDs. We are going to add the gene IDs of orthologous genes in mouse to the corresponding human genes in the module table.

Orthology mapping can be tricky, but thankfully Wan et al have already identified mouse orthologs for each of the human genes using the HGNC Comparison of Orthology Predictions (HCOP) tool. While there are a variety of different ways to get data about gene orthology, for the sake of simplicity we are going to read that table from Synapse.

R

mouse.human.ortho <- fread(synapser::synGet("syn17010253")$path,check.names = F,header=T)

Let’s take a look at the first few rows of this orthology table:

R

head(mouse.human.ortho)

There are 15 columns with various gene identifiers for each species. We’ll add mouse gene symbols from the ortholog table to the module table by matching the human ENSEMBL IDs from both tables.

R

module_table$Mouse_gene_name <-
  mouse.human.ortho$mouse_symbol[
    match(module_table$GeneID,mouse.human.ortho$human_ensembl_gene)
    ]

Taking a look at the module table, we can see the new column of mouse orthologs we just added.

R

head(module_table)

Some genes don’t have identified orthologs. Also there’s some redundant information. Let’s only keep the columns of interest and rows that contain a mouse ortholog mapping:

R

ampad_modules <- module_table %>%
  distinct(tissue = brainRegion, module = Module, gene = GeneID, Mouse_gene_name) %>%
  filter(Mouse_gene_name != "")

Take a look at this new data table:

R

head(ampad_modules)

Challenge 2

How many human genes are we removing that don’t have identified orthologs?

Show me the solution

R

dplyr::filter(module_table, is.na(Mouse_gene_name)) %>% 
  dplyr::select(external_gene_name) %>% 
  dplyr::distinct() %>% 
  nrow()

Reading differential expression result of human data from meta-analysis

Now we know the genes that are in each AMP-AD co-expression cluster, along with the ID of the corresponding orthologous gene in mouse. We’ll also need to know how these genes change expression in AD.

We’ll download the results from differential expression meta-analysis of reprocessed AMP-AD RNA-seq data (all 7 brain regions). Log fold change values for human transcripts can be obtained from Synapse.

R

ampad_modules_raw <- fread(synapser::synGet("syn14237651")$path,check.names = F,header=T)

Let’s take a look at these data

R

head(ampad_modules_raw)

Data from which tissues are in this table?

R

unique(ampad_modules_raw$Tissue)

All 7 brain regions are represented.

The AMP-AD data has been processed many ways and using different models and comparisons. Let’s take a look at how many ways the data have been analyzed:

R

ampad_modules_raw %>% select(Model, Comparison) %>% distinct()

For our analyses we’ll use data from the “Diagnosis” model and comparisons between AD cases vs controls. We’ll filter the table for these conditions and only keep the three columns we’ll need: Tissue, Gene and logFC.

R

ampad_fc <- ampad_modules_raw %>%
  as_tibble() %>%
  filter(Model == "Diagnosis", Comparison == "AD-CONTROL") %>%
  dplyr::select(tissue = Tissue, gene = ensembl_gene_id, ampad_fc = logFC) %>% 
  distinct()

Combine with modules so correlation can be done per module

Next, we will combine the fold change table we just downloaded (ampad_fc) and module table from before (ampad_modules). First, let’s look at both tables to check how can we merge them together?

R

head(ampad_fc)
head(ampad_modules)

The columns common to both tables are gene (the human Ensembl gene IDs) and tissue (the brain region corresponding to the module/measurement). So we will merge the data sets using these two columns.

Reminder: Each gene can be present in multiple brain regions, but should only be in one module per brain region. Let’s double check using the first gene in the table:

R

ampad_modules[ampad_modules$gene %in% "ENSG00000168439",]

This gene is present in six different co-expression modules all from different brain regions. You can do this for any other gene as well.

We’ll merge the two tables using the dplyr::inner_join function:

R

ampad_modules_fc <- inner_join(ampad_modules, ampad_fc, by = c("gene", "tissue")) %>% 
  dplyr::select(symbol = Mouse_gene_name, module, ampad_fc)

Take a look at the new table we just made:

R

head(ampad_modules_fc)

We will use the data in ampad_modules_fc to compare with log fold change data measured in mouse models.

Preparing module information for correlation plots

Let’s package up these data and save this progress so far. This is some manual book-keeping to arrange the modules into consensus clusters for plotting later. You can just copy-paste this code into your Rstudio session.

R

cluster_a <- tibble(
  module = c("TCXblue", "PHGyellow", "IFGyellow"),
  cluster = "Consensus Cluster A (ECM organization)",
  cluster_label = "Consensus Cluster A\n(ECM organization)"
)

cluster_b <- tibble(
  module = c("DLPFCblue", "CBEturquoise", "STGblue", "PHGturquoise", "IFGturquoise", "TCXturquoise", "FPturquoise"),
  cluster = "Consensus Cluster B (Immune system)",
  cluster_label = "Consensus Cluster B\n(Immune system)"
)

cluster_c <- tibble(
  module = c("IFGbrown", "STGbrown", "DLPFCyellow", "TCXgreen", "FPyellow", "CBEyellow", "PHGbrown"),
  cluster = "Consensus Cluster C (Neuronal system)",
  cluster_label = "Consensus Cluster C\n(Neuronal system)"
)

cluster_d <- tibble(
  module = c("DLPFCbrown", "STGyellow", "PHGgreen", "CBEbrown", "TCXyellow", "IFGblue", "FPblue"),
  cluster = "Consensus Cluster D (Cell Cycle, NMD)",
  cluster_label = "Consensus Cluster D\n(Cell Cycle, NMD)"
)

cluster_e <- tibble(
  module = c("FPbrown", "CBEblue", "DLPFCturquoise", "TCXbrown", "STGturquoise", "PHGblue"),
  cluster = "Consensus Cluster E (Organelle Biogensis, Cellular stress response)",
  cluster_label = "Consensus Cluster E\n(Organelle Biogenesis,\nCellular stress response)"
)

module_clusters <- cluster_a %>%
  bind_rows(cluster_b) %>%
  bind_rows(cluster_c) %>%
  bind_rows(cluster_d) %>%
  bind_rows(cluster_e) %>%
  mutate(cluster_label = fct_inorder(cluster_label))

head(module_clusters)

mod <- module_clusters$module

save(ampad_modules_fc,module_clusters,mod,file="../data/AMPAD_Module_Data.RData")

Correlation between mouse models and human AD modules

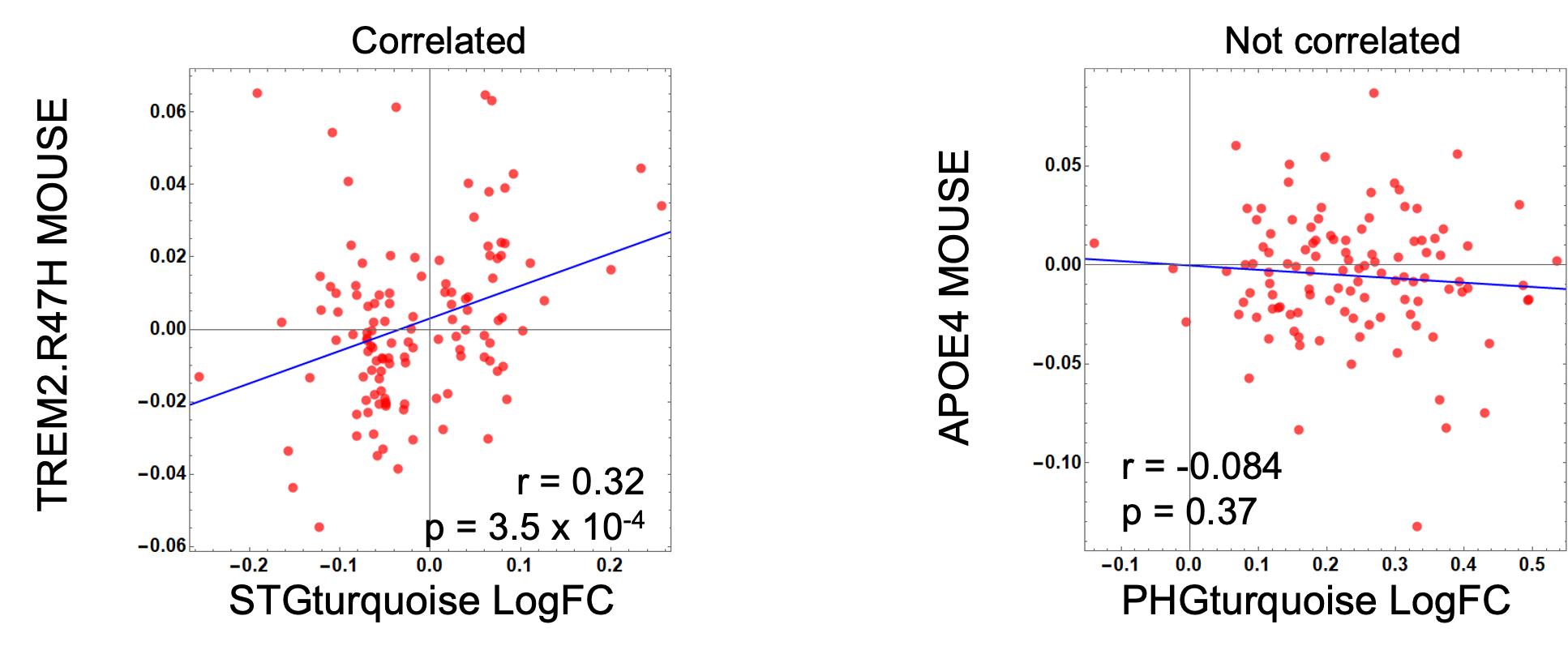
As demonstrated in the plots below, we’ll aim to identify modules where the gene expression is correlated between human and mouse orthologs (left) as well as modules where there is no correlation (right).

There are two approaches that we commonly use to compute correlation between mouse data and human AD data:

Compare change in expression in Human AD cases vs controls with change in expression in mouse models for each gene in a given module:

LogFC(h) = log fold change in expression of human AD patients compared to control patients.
LogFC(m) = log fold change in expression of mouse AD models compared to control mouse models.

\[cor.test(LogFC(h), LogFC(m))\]

Compare Human AD expression changes to mouse genetic effects for each gene in a given module:

h = human gene expression (Log2 RNA-seq Fold Change AD/control)
β = mouse gene expression effect from linear regression model (Log2 RNA-seq TPM)

\[cor.test(LogFC(h), β)\]

Both approaches allow us to assess directional coherence between gene expression for genes in AMP-AD modules and the effects of genetic manipulations in mice. For this lesson we are going to use the first approach.

Step 0: Reading Gene Expression Count matrix from Previous Lesson

We’ll first read the result table saved after differential analysis in last lesson. We’ll start with the data from the 5xFAD mouse model to understand the required steps to perform the correlation with human AD modules.

R

load("results/DEAnalysis_5XFAD.Rdata")

We can also load AMP-AD module data.

R

load("data/AMPAD_Module_Data.RData")

Step 1: Measure the correlation between mouse models for each sex at each age and AMP-AD modules using common genes from both datasets

We compute a Pearson correlation between changes in expression for each gene within a given module (log fold change for cases vs controls) with each mouse model (log fold change of the 5xFAD mice vs sex- and age-matched B6 mice).

First, we’ll combine both mouse DE_5xFAD.df and human ampad_modules_fc log fold change data sets for all genes.

R

model_vs_ampad <- inner_join(DE_5xFAD.df, ampad_modules_fc, by = c("symbol"), multiple = "all")

Note: for this join we specify multiple = "all" so that the same gene can be matched across multiple human tissues.

R

head(model_vs_ampad)

Now we’ll create a list column containing data frames using tidyr::nest function. Nesting is implicitly a summarizing operation: you get one row for each group defined by the non-nested columns.

R

df <- model_vs_ampad %>%
  dplyr::select(module, model, sex, age, symbol, log2FoldChange, ampad_fc) %>%
  group_by(module, model, sex, age) %>%
  nest(data = c(symbol, log2FoldChange, ampad_fc))

Let’s take a look:

R

head(df)

And we can also look at some of the nested data:

R

head(df$data[[1]])

These are the mouse and human log fold-change values for all genes in the TCXblue module; the mouse data corresponds to 4 month old male 5xFAD mice.

The total number of groups in the data table:

R

dim(df)

Next, we’ll compute correlation coefficients using the cor.test function:

R

cor.df <- df  %>%
  mutate(
      cor_test = map(data, ~ cor.test(.x[["log2FoldChange"]], 
                                      .x[["ampad_fc"]], method = "pearson")),
      estimate = map_dbl(cor_test, "estimate"),
      p_value = map_dbl(cor_test, "p.value")
      ) %>%
  ungroup() %>%
  dplyr::select(-cor_test)

Here we’re using purrr::map based functions to apply the correlation test to every entry in the data column. We can pull out specific features from the cor_test list column, including the computed correlation coefficient (estimate) and the significance (p.value).

In the end we should have correlation coefficients and significance values for every comparison in our data table:

R

head(cor.df)

Step 2: Annotate correlation table to prepare for visualization

These steps will make it easier to make a nice looking plot during the next step. We’ll add a column that flags whether the correlation is significant or not, and we’ll add in the information about which consensus cluster each module belongs to:

R

model_module <- cor.df %>%
  mutate(significant = p_value < 0.05) %>%
  left_join(module_clusters, by = "module") %>%
  dplyr::select(cluster, cluster_label, module, model, sex, age,
                correlation = estimate, p_value, significant)

R

head(model_module)

Step 3: Create a dataframe to use as input for plotting the results

More preparations for plotting, here we’ll get all of the values in the right order so that they are grouped together nicely on the plot.

R

order.model <- c("5xFAD (Male)", "5xFAD (Female)")

correlation_for_plot <- model_module %>%
    arrange(cluster) %>%
    mutate(
      module = factor(module,levels=mod),
      model_sex = glue::glue("{model} ({str_to_title(sex)})"),
    ) %>%
    arrange(model_sex) %>%
    mutate(
      age = factor(age, levels = c('4 mo','6 mo', '12 mo')),
      model_sex = factor(model_sex,levels=order.model),
      model_sex = fct_rev(model_sex),
    )

head(correlation_for_plot)

Visualizing the Correlation plot

Now, we will use the above matrix and visualize the correlation results using ggplot2 package functions.

R

data <- correlation_for_plot
range(correlation_for_plot$correlation)

ggplot2::ggplot() +
  
  # the AMP-AD modules will be along the x-axis, the mouse models will be along the y-axis
  ggplot2::geom_tile(data = data, ggplot2::aes(x = .data$module, y = .data$model_sex), colour = "black", fill = "white") +
  
  # each tile of the grid will be filled with a circle where the fill and size correspond to the correlation coefficient
  ggplot2::geom_point(data = dplyr::filter(data), ggplot2::aes(x = .data$module, y = .data$model_sex, colour = .data$correlation, size = abs(.data$correlation))) +
  
  # we'll draw a box arround significant correlations
  ggplot2::geom_point(data = dplyr::filter(data, .data$significant), ggplot2::aes(x = .data$module, y = .data$model_sex, colour = .data$correlation),color="black",shape=0,size=9) +
  
  # plot the x-axis on the top of the plot, set the parameters of the scales
  ggplot2::scale_x_discrete(position = "top") +
  ggplot2::scale_size(guide = "none", limits = c(0, 0.4)) +
  ggplot2::scale_color_gradient2(limits = c(-0.5, 0.5), low = "#85070C", high = "#164B6E", name = "Correlation", guide = ggplot2::guide_colorbar(ticks = FALSE)) +
  
  # remove axis labels
  ggplot2::labs(x = NULL, y = NULL) +
  
  # facet the plot based on age range for the mice (rows) and consensus cluster (columns)
  ggplot2::facet_grid( rows = dplyr::vars(.data$age),cols = dplyr::vars(.data$cluster_label), scales = "free", space = "free",switch = 'y') +
  
  # specify how different aspects of the plot will look
  ggplot2::theme(
    strip.text.x = ggplot2::element_text(size = 10,colour = c("black")),
    strip.text.y.left = ggplot2::element_text(angle = 0,size = 12),
    axis.ticks = ggplot2::element_blank(),
    axis.text.x = ggplot2::element_text(angle = 90, hjust = 0, size = 12),
    axis.text.y = ggplot2::element_text(angle = 0, size = 12),
    panel.background = ggplot2::element_blank(),
    plot.title = ggplot2::element_text(angle = 0, vjust = -54, hjust = 0.03,size=12,face="bold"),
    plot.title.position = "plot",
    panel.grid = ggplot2::element_blank(),
    legend.position = "right"
  )

In the above plot, categories along the x-axis are the 30 AMP-AD co-expression modules grouped into 5 consensus clusters, while the categories along the y-axis show the different groupings of mouse models tested (split by age and sex). Positive correlations are shown in blue and negative correlations in red. Color intensity and size of the circles are proportional to the correlation coefficient. Black squares around dots represent significant correlation at p-value=0.05 and non-significant correlations are left blank.

Male and female 5xFAD mice display gene expression alterations across all five consensus clusters, with the strongest correlations observed among modules/genes in Consensus Cluster B, which generally consists of immune system pathways and functions.

Examining individual correlation results

Let’s say we want to know more about a single comparison in the plot above and which genes are contributing to the correlation result. Maybe we’re really interested in the correlations to the FPbrown module between female 5xFAD mice at 4 months and 6 months. We can plot the individual correlations for each comparison in the plot above with the data we have. We’ll label genes with large fold change in the mouse using the ggrepel::geom_label_repel function.

R

# specify which comparisons to consider
m <- 'FPbrown'
s <- 'female'
a <- c('4 mo','6 mo')

# filter the correlation data frame to these comparisons
indiv.corr <- cor.df %>% filter(module == m, sex == s, age %in% a) %>% unnest(data) %>% 
  mutate( facet = str_c(age, '\n', 'r = ',signif(estimate,3),' ; p = ',signif(p_value,3) ))

# plot
ggplot(indiv.corr, aes( log2FoldChange , ampad_fc ))+
  geom_vline(xintercept = 0, lwd = .1)+
  geom_hline(yintercept = 0, lwd = .1)+
  geom_point( size = .5, color = 'darkred')+
  geom_smooth(method = 'lm', lwd = .5)+
  ggrepel::geom_label_repel( data = arrange(indiv.corr, desc(abs(log2FoldChange))), 
                             aes(label = symbol), size = 2 ) +
  labs(x = '5xFAD logFC', y = 'AMP-AD logFC',
       title = unique(indiv.corr$module))+
  facet_wrap(~facet)+
  theme_bw()

Here we can see that the 5xFAD logFC are pretty small in general. The correlations are relatively weak and driven by individual genes that have relatively large changes (e.g. Heatr4, Nirp1a, Rpl39l). If we compare a different module, say STGblue, we can see a stronger relationship between the mouse and human expression.

R

m <- 'STGblue'
s <- 'female'
a <- c('4 mo','12 mo')

indiv.corr <- cor.df %>% filter(module == m, sex == s, age %in% a) %>% unnest(data) %>% 
  mutate( v = str_c(age, '\n', 'r = ',signif(estimate,3),' ; p = ',signif(p_value,3) ))

ggplot(indiv.corr, aes( log2FoldChange , ampad_fc ))+
  geom_vline(xintercept = 0, lwd = .1)+
  geom_hline(yintercept = 0, lwd = .1)+
  geom_point( size = .5, color = 'darkred')+
  geom_smooth(method = 'lm', lwd = .5)+
  ggrepel::geom_label_repel( data = arrange(indiv.corr, desc(abs(log2FoldChange))), 
                             aes(label = symbol), size = 2 ) +
  labs(x = '5xFAD logFC', y = 'AMP-AD logFC',
       title = unique(indiv.corr$module))+
  facet_wrap(~v)+
  theme_bw()

These correlations are much stronger (r ~ 0.3 vs 0.1 in the previous example), and there is a consistent pattern between young mice and old mice, with similar genes being expressed in similar ways (e.g. Itgax and Clec7a are up-regulated at both ages). We also saw in the Volcano plot that immune-related genes were significantly up-regulated in the 5xFAD model. These significant positive correlation suggests that the 5xFAD model captures inflammatory changes observed in human AD patients.

Challenge 3

Considering the LOAD1 (i.e. APOE4.Trem2) model results, which modules show correlation and how does it compare with 5xFAD?

Show me the solution

R

 load("fig/DEAnalysis_LOAD1.Rdata")
 model_vs_ampad <- inner_join(DE_LOAD1.df, ampad_modules_fc, by = c("symbol"), multiple = "all") 
 cor.df <- model_vs_ampad %>%
   dplyr::select(module, model, sex, age, symbol, log2FoldChange, ampad_fc) %>%
   group_by(module, model, sex, age) %>%
   nest(data = c(symbol, log2FoldChange, ampad_fc)) %>% 
   mutate(
       cor_test = map(data, ~ cor.test(.x[["log2FoldChange"]], 
                                       .x[["ampad_fc"]], method = "pearson")),
       estimate = map_dbl(cor_test, "estimate"),
       p_value = map_dbl(cor_test, "p.value")
       ) %>%
   ungroup() %>%
   dplyr::select(-cor_test)
 model_module <- cor.df %>%
     mutate(significant = p_value < 0.05) %>%
     left_join(module_clusters, by = "module") %>%
     dplyr::select(cluster, cluster_label, module, model, sex, age,
                   correlation = estimate, p_value, significant)
 order.model <- c("APOE4 (Male)", "APOE4 (Female)","Trem2 (Male)", "Trem2 (Female)","APOE4Trem2 (Male)", "APOE4Trem2 (Female)")
 correlation_for_plot <- model_module %>%
     arrange(cluster) %>%
     mutate(
       module = factor(module,levels=mod),
       model_sex = glue::glue("{model} ({str_to_title(sex)})"),
    ) %>%
     arrange(model_sex) %>%
     mutate(
       age = factor(age, levels = c(4,8)),
       model_sex = factor(model_sex,levels=order.model),
       model_sex = fct_rev(model_sex),
     )
 data <- correlation_for_plot
 ggplot2::ggplot() +
   ggplot2::geom_tile(data = data, ggplot2::aes(x = .data$module, y = .data$model_sex), colour = "black", fill = "white") +
   ggplot2::geom_point(data = dplyr::filter(data), ggplot2::aes(x = .data$module, y = .data$model_sex, colour =  .data$correlation, size = abs(.data$correlation))) +
   ggplot2::geom_point(data = dplyr::filter(data, .data$significant), ggplot2::aes(x = .data$module, y = .data$model_sex, colour = .data$correlation),color="black",shape=0,size=9) +
   ggplot2::scale_x_discrete(position = "top") +
   ggplot2::scale_size(guide = "none", limits = c(0, 0.4)) +
   ggplot2::scale_color_gradient2(limits = c(-0.5, 0.5), low = "#85070C", high = "#164B6E", name = "Correlation", guide = ggplot2::guide_colorbar(ticks = FALSE)) +
   ggplot2::labs(x = NULL, y = NULL) +
   ggplot2::facet_grid( rows = dplyr::vars(.data$age),cols = dplyr::vars(.data$cluster_label), scales = "free", space = "free",switch = 'y') +
   ggplot2::theme(
     strip.text.x = ggplot2::element_text(size = 10,colour = c("black")),
     strip.text.y.left = ggplot2::element_text(angle = 0,size = 12),
     axis.ticks = ggplot2::element_blank(),
     axis.text.x = ggplot2::element_text(angle = 90, hjust = 0, size = 12),
     axis.text.y = ggplot2::element_text(angle = 0, size = 12),
     panel.background = ggplot2::element_blank(),
     plot.title = ggplot2::element_text(angle = 0, vjust = -54, hjust = 0.03,size=12,face="bold"),
     plot.title.position = "plot",
     panel.grid = ggplot2::element_blank(),
     legend.position = "right"
   )

The LOAD1 models show weaker correlation to AMP-AD module gene expression overall, and in particular anti-correlation for Consensus Cluster B (immune) modules.

Detecting functional coherence of gene sets from omics data

Most omics analyses produce data on many thousands of genomic features (i.e. transcripts, proteins, etc.) for each condition tested. Simply looking at these lists of genes and associated statistics can be daunting and uninformative. We need approaches to identify which biological functions are being impacted by a given experiment from these systems-level measurements.

Gene functional enrichment analysis describes a variety of statistical methods that identify groups of genes that share a particular biological function or process and show differential association with experimental conditions. Most approaches compare some statistically valid set of differentially expressed features to sets of functional annotations for those features. There are many different functional annotation sets available, some of the more commonly used include:

gene function resources, such as the Gene Ontology (i.e. GO)
pathway databases, such as Reactome or KEGG
disease and phenotype ontologies, such as the Human Phenotype Ontology, the Mammalian Phenotype Ontology, and the Disease Ontology

These are the resources that are the foundation for many genomics knowledge bases, such as MGI, monarch initiative, and the Alliance of Genome Resources. The precise nature of each of these resources varies, but the core information contained within each is the relationship of sets of genes to biologically meaningful annotations. These annotations are typically expertly curated from the published literature.

There are a variety of statistical approaches that can be employed to test for functional enrichment among genes identified from an omics dataset. Two of the most common broad classes of tests are over-representation analysis (ORA) and gene set enrichment analysis (GSEA). For example, consider the figure below from Zhao & Rhee, Trends in Genetics (2023). Let’s consider each in a bit more detail.

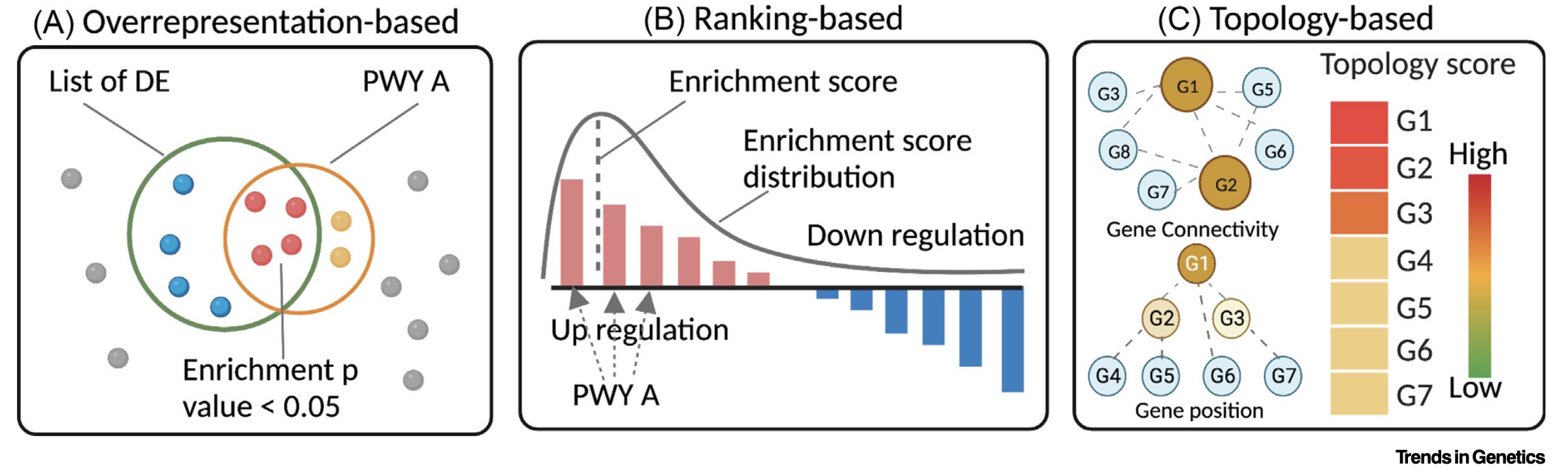
Over-representation analysis

ORA involves statistical tests of overlap between two lists of genes: one derived from the experiment and one from the functional annotations. For example, one might ask what is the overlap between the genes in an annotation class, such as “Lysosome”, and the genes that are significantly up-regulated in a given experimental condition. These tests usually rely on some form of Fisher’s exact test (e.g. fisher.test()) or hypergeometric test (e.g. phyper()). If the gene lists consist of a larger number of overlapping genes than would be expected at random - given the sample sizes involved - then there is said to be a statistical over-representation of the annotation class within the experimental condition.

Of course, these overlap tests are generally considered for all annotation classes, which can number in the hundreds to thousands. Performing this many statistical tests ensures that many will be identified as significant by chance. Therefore, there is typically a requirement to correct for multiple testing errors (e.g. p.adjust()).

There are many R packages available to handle the statistical tests and corrections involved in ORA. Today we’ll use clusterProfiler::enrichGO(), which wraps statistical testing for overlap with GO terms and multiple test correction in one function.

Let’s start by considering the enrichments from the mouse data analyzed previously.

R

theme_set(theme_bw())
load('results/DEAnalysis_5XFAD.RData')

We’ll start by considering the genes that are significantly DE in 12 month old male animals

R

gene.list.up <- DE_5xFAD.df %>% 
  filter(sex == 'male', 
         age == '12 mo',
         padj <= 0.05, 
         log2FoldChange > 0) %>%
  arrange(desc(log2FoldChange)) %>% 
  filter(!duplicated(symbol), !is.na(symbol)) %>% 
  pull(symbol) %>% 
  unique()

gene.list.dn <- DE_5xFAD.df %>% 
  filter(sex == 'male', 
         age == '12 mo',
         padj <= 0.05, 
         log2FoldChange < 0) %>%
  arrange(desc(log2FoldChange)) %>% 
  filter(!duplicated(symbol), !is.na(symbol)) %>% 
  pull(symbol) %>% 
  unique()

length(gene.list.up)
length(gene.list.dn)

There are a total of significantly up-regulated genes and significantly down-regulated genes in this cohort. Now test for over representation of GO terms among the DEGs. First, we need to identify the universe of all possible genes which includes the genes that were both measured by the experiment and contained within the annotation set.

R

univ <- as.data.frame(org.Mm.egGO) %>% 
  pull(gene_id) %>% 
  unique() %>% 
  bitr(., fromType = "ENTREZID", toType = 'SYMBOL', OrgDb = org.Mm.eg.db, drop = T) %>% 
  pull('SYMBOL') %>% 
  intersect(., DE_5xFAD.df$symbol)

Now let’s test for enriched GO terms (this can take 3-4 minutes)

R

enr.up <- enrichGO(gene.list.up, 
                   ont = 'all', 
                   OrgDb = org.Mm.eg.db, 
                   keyType = 'SYMBOL',
                   universe = univ
                   )
enr.dn <- enrichGO(gene.list.dn, 
                   ont = 'all', 
                   OrgDb = org.Mm.eg.db, 
                   keyType = 'SYMBOL',
                   universe = univ
                   )

How many significant terms are identified:

R

enr.up@result %>% filter(p.adjust <= 0.05) %>% pull(ID) %>% unique() %>% length()
enr.dn@result %>% filter(p.adjust <= 0.05) %>% pull(ID) %>% unique() %>% length()

Challenge 4

How many significant terms are identified from the up-regulated gene list if you do not specify the “universe”?

Show me the solution

R

 enrichGO(gene.list.up, ont = 'all', OrgDb = org.Mm.eg.db, keyType = 'SYMBOL') %>% 
   .@result %>% filter(p.adjust <= 0.05) %>% pull(ID) %>% unique() %>% length()

Plot the top 10 significant terms:

R

cowplot::plot_grid(
  dotplot(enr.dn, showCategory = 10) + ggtitle('down'),
  dotplot(enr.up, showCategory = 10) + ggtitle('up')
)

From this we can see that nervous system related terms (e.g. “learning or memory”, “neurotransmitter transport”) are down in 5xFAD males at 12 months, while immune functions (e.g. “cytokine-mediated signaling pathway” and “leukocyte mediated immunity”) are up in 5xFAD males at 12 months.

Gene set enrichment analysis

GSEA is an alternative approach that uses a statistical measure from the omics data (e.g. the log fold change or significance) to rank the genes. An “enrichment score” is calculated for each annotation set based on where the genes annotated to the term sit in the overall distribution.

Let’s analyze those same data with the clusterProfiler::gseGO() function. First we’ll specify the gene list and use the log2FoldChange value to rank the genes in the list.

R

gene.list <- DE_5xFAD.df %>% 
  filter(sex == 'male', 
         age == '12 mo',
         padj <= 0.05
         ) %>%
  arrange(desc(log2FoldChange)) %>% 
  filter(!duplicated(symbol), !is.na(symbol)) %>% 
  pull(log2FoldChange, name = symbol)

Now we’ll test for enrichment:

R

enr <- gseGO(gene.list, ont = 'all', OrgDb = org.Mm.eg.db, keyType = 'SYMBOL')

How many significant terms are identified:

R

enr@result %>% filter(p.adjust <= 0.05) %>% pull(ID) %>% unique() %>% length()

Challenge 5

The tally above represents all genes, both up- and down-regulatd. To compare between GSEA and ORA, can you identify how many GSEA enriched terms are associated with up-regulated genes and how many are associated with down-regulated genes? (Hint: the NES value within the results relates to the directionality of enrichment).

Show me the solution

R

 enr@result %>% filter(p.adjust <= 0.05, NES < 0) %>% pull(ID) %>% unique() %>% length()  
 enr@result %>% filter(p.adjust <= 0.05, NES > 0) %>% pull(ID) %>% unique() %>% length()

Plot the term enrichments

R

ridgeplot(enr, core_enrichment = T, showCategory = 15)

This plot shows the top 15 GSEA enriched terms. The displayed terms are all from the up-regulated class (i.e. NES > 0), and consist of many immune-relevant terms (e.g. “immune response” and “cytokine production”).

Common pitfalls & best practices

These kinds of functional enrichment analyses are very common, but not all results reported are equal! A recent paper describes an “Urgent need for consistent standards in functional enrichment analysis”. They examine how the results of functional enrichment analyses are reported in the literature, and identify several common shortcomings. Watch out for these common mistakes when performing and reporting your own analyses!

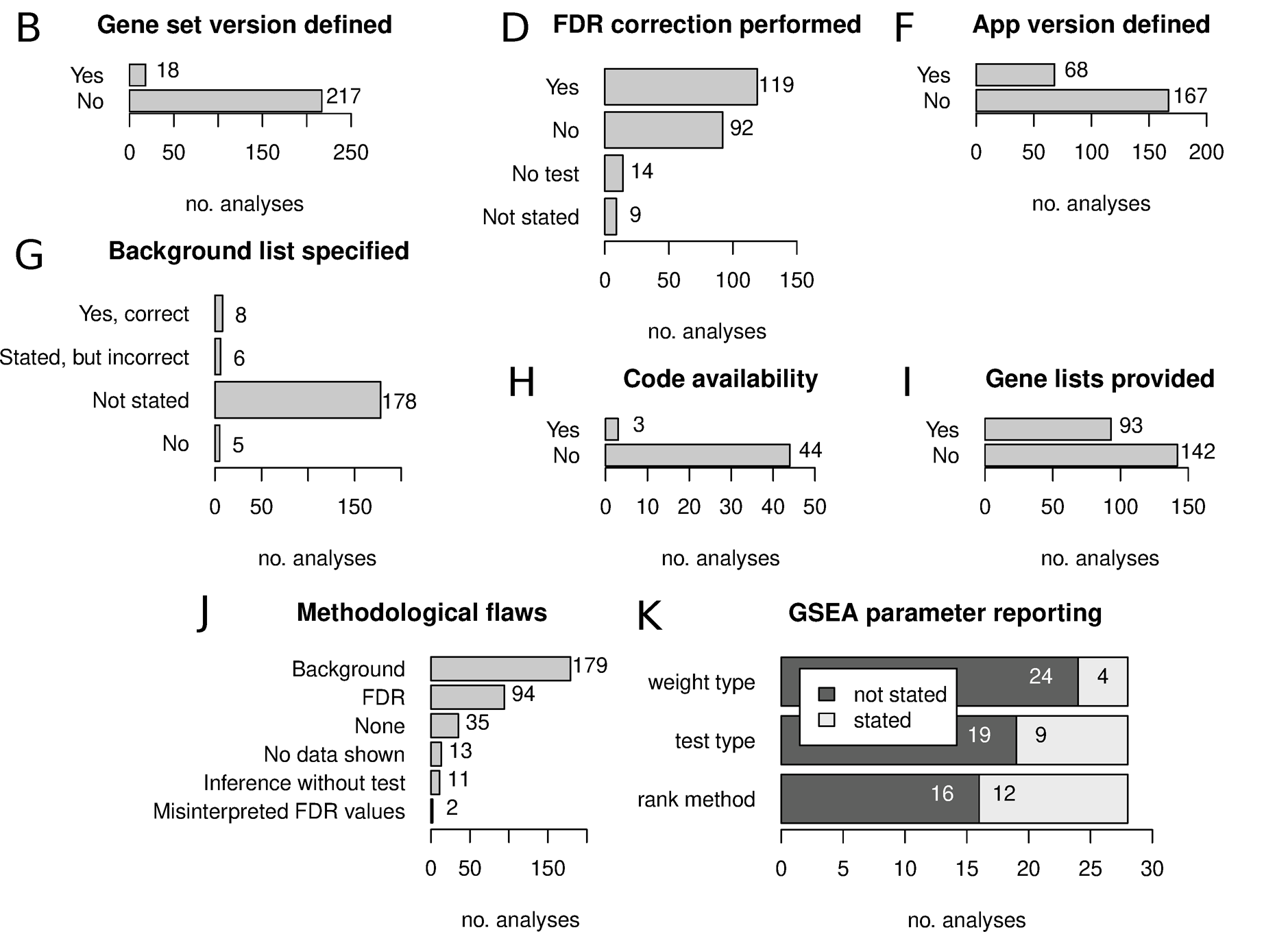
Alzheimers’s Disease Biological Domains

While these results are informative and help to provide essential biological context to the results of the omics experiment, it is difficult to understand all of the enriched terms and what that means for the biology of disease. It would be useful to group each of the enriched terms within broader areas of disease biology. There are several common molecular endophenotypes that are detected within human Alzheimer’s cohorts across omics data types (transcriptomics, proteomics, and genetics). Several of these endophenotypic areas are shown in the figure below (source: Jesse Wiley).

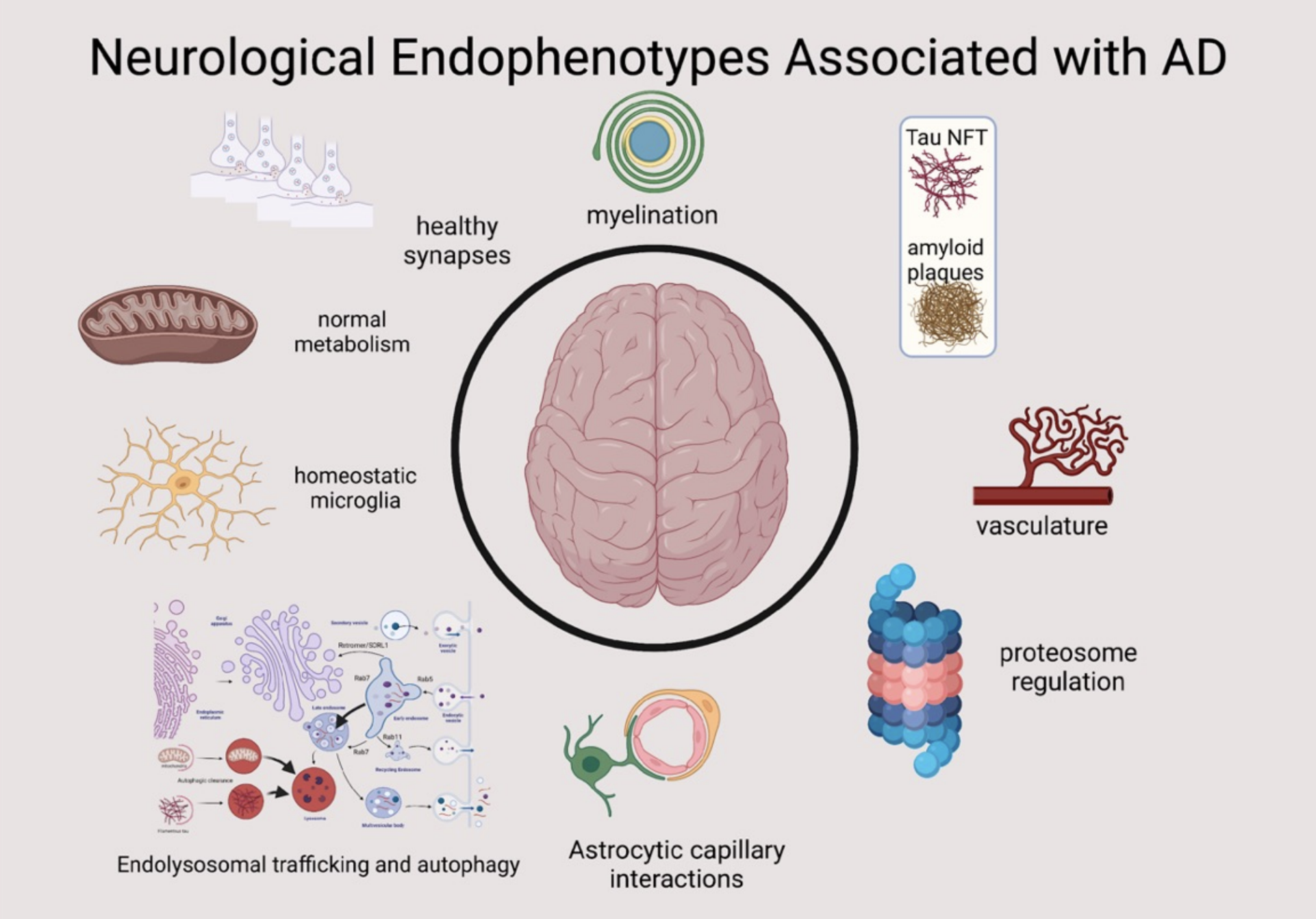
These endophenotypes describe molecular processes that are dysregulated by or during the disease process. Very similar sets of endophenotypes have been cataloged among the targets of therapeutics in clinical trials for AD (see below, Cummings et al, Alzheimer’s disease drug development pipeline: 2023, Alz Dem TRCI.

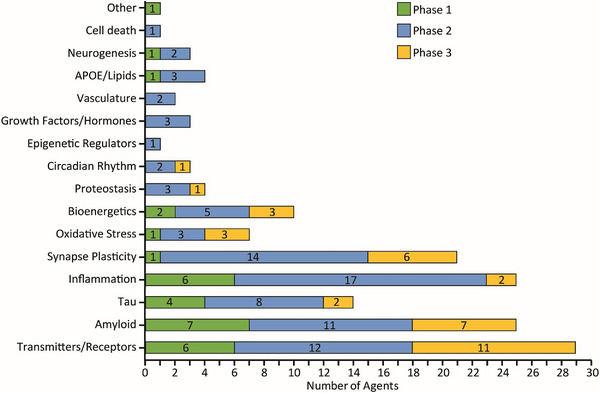
In order to formalize and operationalize these endophenotypic areas, the Emory-Sage-SGC center of the TREAT-AD consortium has developed the Biological Domains of AD. In the enumeration of these domains, several criteria were established; the biological domains defined should be:

objective: leverage existing well-annotated resources
automatable: in CADRO, therapeutics and targets are manually assigned
intelligible: groupings should be easy to understand
modifiable: definitions should be (and are!) continuously be updated.

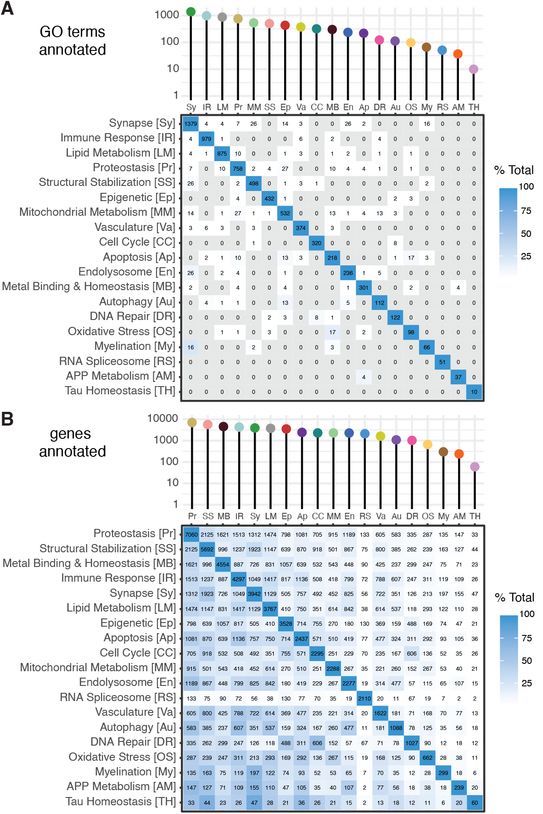
In all, 19 distinct biological domains (aka biodomains) have been identified. These biological domains are defined using sets of GO terms that align with the endophenotype. For example, terms like “cytokine receptor binding” and “leukocyte migration” are annotated to the Immune Response biodomain, while terms like “postsynaptic density” and “synaptic vesicle cycle” are annotated to the Synapse biodomain. Of all terms in the GO, 7,127 terms (16.4%) are annotated to one of the biological domains. Because the GO terms have genes annotated, genes can be associated with specific endophenotypes via the biological domain groupings of terms. In all, 18,289 genes are annotated to at least 1 biodomain term. While the biodomains exhibit very few overlapping GO terms (panel A), due to gene pleiotropy (etc) the number of overlapping genes between biological domains is quite a bit higher (panel B). The development of the biological domains is described in more detail in the published paper Genetic and Multi-omic Risk Assessment of Alzheimer’s Disease Implicates Core Associated Biological Domains.

Download and explore the biological domain annotations

First let’s download the biodomain definition file from synapse.

R

#synLogin()

# biodomain definitions
biodom <- readRDS(synGet('syn25428992')$path)
dom.lab <- read_csv(synGet('syn26856828')$path)

What is in the file?

R

head(biodom)

You can see the file is a list of GO term accessions (GO_ID) and names (GOterm_Name) as well as the corresponding endophenotype (Biodomain) to which the term is annotated. There are also gene annotations for each term. These annotation sets come from two sources: (1) the symbol and uniprot annotations are drawn directly from the Gene Ontology via the provided API, (2) ensembl_id, entrez_id, and hgnc_symbol are from BioMart annotations (e.g. biomaRt::getLDS()).

We can see how many GO terms are annotated to each biodomain:

R

biodom %>% group_by(Biodomain) %>% summarise(n_term = length(unique(GO_ID))) %>% arrange(n_term)

The biodomains range in size from Tau Homeostasis (10 terms) up to Synapse (1,379 terms).

We can also investigate the individual genes annotated to each biodomain GO term.

R

biodom %>% filter(GOterm_Name == 'amyloid-beta formation') %>% pull(symbol) %>% unlist()

So the genes associated with amyloid-beta formation within the APP Metabolism biodomain include PSEN1, PSEN2, BACE1, ABCA7, NCSTN, and others.

Annotate enriched terms with biological domain

Let’s re-characterize the 5xFAD functional enrichments we computed previously with the biological domain annotations and see if we can get more context about what is changing in that model. We’ll focus on the GSEA results and start by annotating the results with biodomain groupings.

R

enr.bd = enr@result %>% 
  left_join(., biodom %>% select(Biodomain, ID = GO_ID), by = 'ID') %>% 
  relocate(Biodomain)

head(enr.bd[,1:4])

Not all of the enriched terms are annotated to a biological domain. Some terms are too broad and not specific (e.g. ‘defense response’), while others may not have been captured by a biological domain annotation yet (e.g. ‘regulation of immune system process’). Remember that the conception of the biodomains involved a requirement that they be modifiable, and these terms may be added to the biodomain definintions in the future. Let’s modify the Biodomain value for terms that aren’t annotated to a domain to ‘none’.

R

enr.bd$Biodomain[is.na(enr.bd$Biodomain)] <- 'none'
head(enr.bd[,1:4])

How many terms are enriched from each domain?

R

bd.tally = tibble(domain = c(unique(biodom$Biodomain), 'none')) %>% 
  rowwise() %>% 
  mutate(
    n_term = biodom$GO_ID[ biodom$Biodomain == domain ] %>% unique() %>% length(),
    n_sig_term = enr.bd$ID[ enr.bd$Biodomain == domain ] %>% unique() %>% length()
    )
arrange(bd.tally, desc(n_sig_term))

Many enriched terms don’t map to a domain (), but most do (). Of those that do, the vast majority map into the Immune Response biodomain.

We can plot the enrichment results, stratified by biodomain:

R

enr.bd_plot <- full_join(enr.bd, dom.lab, by = c('Biodomain' = 'domain')) %>% 
  mutate(Biodomain = factor(Biodomain, levels = arrange(bd.tally, n_sig_term) %>% pull(domain))) %>% 
  arrange(Biodomain, p.adjust) 

ggplot(enr.bd_plot, aes(NES, Biodomain)) +
  geom_violin(data = subset(enr.bd_plot, NES > 0), 
              aes(color = color), scale = 'width')+
  geom_violin(data = subset(enr.bd_plot, NES < 0), 
              aes(color = color), scale = 'width')+
  geom_jitter(aes(size = -log10(p.adjust), fill = color), 
              color = 'grey20', shape = 21, alpha = .3)+
  geom_vline(xintercept = 0, lwd = .1)+
  scale_y_discrete(drop = F)+
  scale_fill_identity()+scale_color_identity()

Challenge 6

How could you plot the results from the ORA to show biodomain enrichements?

Show me the solution

R

 enr.ora = bind_rows(
  enr.up@result %>% mutate(dir = 'up'),
  enr.dn@result %>% mutate(dir = 'dn')
  ) %>% 
  left_join(., biodom %>% select(Biodomain, ID = GO_ID), by = 'ID') %>% 
  relocate(Biodomain)

 enr.ora$Biodomain[is.na(enr.ora$Biodomain)] <- 'none'
 
 bd.tally = tibble(domain = c(unique(biodom$Biodomain), 'none')) %>% 
   rowwise() %>% 
   mutate(
     n_term = biodom$GO_ID[ biodom$Biodomain == domain ] %>% unique() %>% length(),
     n_sig_term = enr.ora$ID[ enr.ora$Biodomain == domain ] %>% unique() %>% length()
     )

 enr.ora <- full_join(enr.ora, dom.lab, by = c('Biodomain' = 'domain')) %>% 
   mutate(Biodomain = factor(Biodomain, levels = arrange(bd.tally, n_sig_term) %>% pull(domain))) %>% 
   arrange(Biodomain, p.adjust) %>% 
   mutate(signed_logP = -log10(p.adjust),
          signed_logP = if_else(dir == 'dn', -1*signed_logP, signed_logP))
   
 ggplot(enr.ora, aes(signed_logP, Biodomain)) +
   geom_violin(data = subset(enr.ora, dir == 'up'), aes(color = color), scale = 'width')+
   geom_violin(data = subset(enr.ora, dir == 'dn'), aes(color = color), scale = 'width')+
   geom_jitter(aes(size = Count, fill = color), color = 'grey20', shape = 21, alpha = .3)+
   geom_vline(xintercept = 0, lwd = .1)+
   scale_y_discrete(drop = F)+
   scale_fill_identity()+scale_color_identity()

Based on the gene list (up or down) we can add a sign to the significance. When we plot this we can see there are many more significantly enriched terms from the ORA. The dominant signal is still the up-regulation of terms from the Immune Response biodomain. There is also nearly exclusive up-regulation of terms from the Autophagy, Metal Binding and Homeostasis, Oxidative Stress, and APP Metabolism domains. The most down-regulated terms are from the Synapse biodomain.

Comparing Human and Mouse functional enrichments

Finally let’s consider how we can compare the functional enrichments in the mouse models with functional enrichments from the AMP-AD cohorts. We can first take a look at the functional enrichments from the different human cohorts. To save some time, let’s load some pre-computed enrichment results for mouse & human data.

R

mm.gsea <- bind_rows(
  read_tsv('data/5xFAD_gsea_results.tsv', col_types = cols()) %>%
    mutate(age = str_remove_all(age, ' mo') %>% as.double()),
  read_tsv('data/LOAD1_gsea_results.tsv', col_types = cols())
)

hs.gsea <- read_tsv('data/Hsap_gsea_results.tsv', col_types = cols())

The cohorts and tissues available are:

R

hs.gsea %>% select(Study, Tissue) %>% distinct()

OUTPUT

# A tibble: 6 × 2
  Study  Tissue
  <chr>  <chr>
1 MAYO   CBE
2 MAYO   TCX
3 MSSM   STG
4 MSSM   PHG
5 MSSM   IFG
6 ROSMAP DLPFC

We can focus on one tissue per cohort, let’s look at TCX for Mayo, PHG for Mt Sinai, and DLPFC for ROSMAP.

R

enr.bd = hs.gsea %>% 
  filter(Tissue %in% c('TCX','PHG','DLPFC')) %>% 
  left_join(., biodom %>% select(Biodomain, ID = GO_ID), by = 'ID') %>% 
  relocate(Biodomain) %>% 
  mutate(Biodomain = if_else( is.na(Biodomain), 'none', Biodomain))

bd.tally = tibble(domain = c(unique(biodom$Biodomain), 'none')) %>% 
  rowwise() %>% 
  mutate(
    n_term = biodom$GO_ID[ biodom$Biodomain == domain ] %>% unique() %>% length(),
    n_sig_term = enr.bd$ID[ enr.bd$Biodomain == domain ] %>% unique() %>% length()
    )

enr.bd <- full_join(enr.bd, dom.lab, by = c('Biodomain' = 'domain')) %>% 
  filter(!is.na(Study)) %>% 
  mutate(Biodomain = factor(Biodomain, levels = arrange(bd.tally, n_sig_term) %>% pull(domain))) %>% 
  arrange(Biodomain, p.adjust)

ggplot(enr.bd, aes(NES, Biodomain)) +
  geom_violin(data = subset(enr.bd, NES > 0), aes(color = color), scale = 'width')+
  geom_violin(data = subset(enr.bd, NES < 0), aes(color = color), scale = 'width')+
  geom_point(aes(size = -log10(p.adjust), fill = color, group = ID), 
              color = 'grey20', shape = 21, alpha = .5, position = position_jitter(width = .25, seed = 2)  )+
  geom_vline(xintercept = 0, lwd = .1)+
  facet_wrap(~paste0(Study, ': ', Tissue))+
  theme(legend.position = 'top')+
  scale_fill_identity()+scale_color_identity()

Huh, the Mayo and MSSM look largely similar, but the ROSMAP DLPFC doesn’t have very many enriched terms. Let’s ignore the ROSMAP result for now and compare the terms enriched between Mayo TCX and the 5xFAD males. First we can join up the enriched terms between the sets into one data frame.

R

comb_5x = bind_rows(
  hs.gsea %>% 
    filter(Study == 'MAYO', Tissue == 'TCX') %>% 
    mutate(species = 'hs') %>% 
    select(ID, Description, species, NES, p.adjust),
  mm.gsea %>% 
    filter(model == '5xFAD', sex == 'male', age == 12) %>% 
    mutate(species = 'mm') %>% 
    select(ID, Description, species, NES, p.adjust)) %>% 
  pivot_wider(id_cols = c(ID, Description), 
              names_from = species, 
              values_from = NES
  ) %>% 
  unnest(cols = c(hs,mm)) %>% 
  mutate(across(c(hs,mm), ~ if_else(is.na(.x), 0, .x)))


head(comb_5x)

OUTPUT

# A tibble: 6 × 4
  ID         Description                                 hs    mm
  <chr>      <chr>                                    <dbl> <dbl>
1 GO:0001568 blood vessel development                  3.20     0
2 GO:0048514 blood vessel morphogenesis                3.18     0
3 GO:0001944 vasculature development                   3.17     0
4 GO:0001525 angiogenesis                              3.16     0
5 GO:0062023 collagen-containing extracellular matrix  3.15     0
6 GO:0042060 wound healing                             3.06     0

Great! Now let’s annotate the biodomains and plot it up:

R

enr.bd <- comb_5x %>% 
  left_join(., biodom %>% select(Biodomain, ID = GO_ID), by = 'ID') %>% 
  relocate(Biodomain) %>% 
  mutate(Biodomain = if_else( is.na(Biodomain), 'none', Biodomain))

bd.tally = tibble(domain = c(unique(biodom$Biodomain), 'none')) %>% 
  rowwise() %>% 
  mutate(
    n_term = biodom$GO_ID[ biodom$Biodomain == domain ] %>% unique() %>% length(),
    n_sig_term = enr.bd$ID[ enr.bd$Biodomain == domain ] %>% unique() %>% length()
    )

enr.bd <- full_join(enr.bd, dom.lab, by = c('Biodomain' = 'domain')) %>% 
  mutate(Biodomain = factor(Biodomain, 
                            levels = arrange(bd.tally, desc(n_sig_term)) %>% pull(domain))) %>% 
  arrange(Biodomain)

ggplot(enr.bd, aes(hs, mm)) +
  geom_point(aes(fill = color),color = 'grey20', shape = 21, alpha = .5)+
  geom_vline(xintercept = 0, lwd = .1)+
  geom_hline(yintercept = 0, lwd = .1)+
  labs(x = 'Mayo TCX\nGSEA NES', y = '12mo male 5xFAD\nGSEA NES')+
  facet_wrap(~Biodomain, scales = 'free')+
  scale_fill_identity()

There are several terms from multiple biodomains that are enriched in similar directions (i.e. from the up-regulated genes in both human AD and 5xFAD). There are fewer that are enriched in opposite directions (i.e. up in human AD and down in 5xFAD, e.g. see Vasculature and Mitochondrial Metabolism), but there are many terms that are unique to either the human or the mouse data set.

Overall, by aligning human and mouse omics signatures through the lens of domains affected in each context, we can get a better understanding of the relationships between the biological processes affected in each context.

Session Info

R

sessionInfo()
R version 4.4.1 (2024-06-14)
Platform: x86_64-pc-linux-gnu
Running under: Ubuntu 22.04.5 LTS

Matrix products: default
BLAS:   /usr/lib/x86_64-linux-gnu/blas/libblas.so.3.10.0 
LAPACK: /usr/lib/x86_64-linux-gnu/lapack/liblapack.so.3.10.0

locale:
 [1] LC_CTYPE=C.UTF-8       LC_NUMERIC=C           LC_TIME=C.UTF-8       
 [4] LC_COLLATE=C.UTF-8     LC_MONETARY=C.UTF-8    LC_MESSAGES=C.UTF-8   
 [7] LC_PAPER=C.UTF-8       LC_NAME=C              LC_ADDRESS=C          
[10] LC_TELEPHONE=C         LC_MEASUREMENT=C.UTF-8 LC_IDENTIFICATION=C   

time zone: UTC
tzcode source: system (glibc)

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
 [1] data.table_1.16.2 lubridate_1.9.3   forcats_1.0.0     stringr_1.5.1    
 [5] dplyr_1.1.4       purrr_1.0.2       readr_2.1.5       tidyr_1.3.1      
 [9] tibble_3.2.1      tidyverse_2.0.0   ggplot2_3.5.1    

loaded via a namespace (and not attached):
 [1] bit_4.5.0        gtable_0.3.6     crayon_1.5.3     compiler_4.4.1  
 [5] renv_1.0.11      tidyselect_1.2.1 parallel_4.4.1   scales_1.3.0    
 [9] yaml_2.3.10      R6_2.5.1         generics_0.1.3   knitr_1.48      
[13] munsell_0.5.1    pillar_1.9.0     tzdb_0.4.0       rlang_1.1.4     
[17] utf8_1.2.4       stringi_1.8.4    xfun_0.48        bit64_4.5.2     
[21] timechange_0.3.0 cli_3.6.3        withr_3.0.1      magrittr_2.0.3  
[25] grid_4.4.1       vroom_1.6.5      hms_1.1.3        lifecycle_1.0.4 
[29] vctrs_0.6.5      evaluate_1.0.1   glue_1.8.0       fansi_1.0.6     
[33] colorspace_2.1-1 tools_4.4.1      pkgconfig_2.0.3

Key Points

AMP-AD gene modules represent major transcriptomic heterogeneity in AD
Correlation of logFC is a practical approach for human-mouse alignment of AD-associated transcriptomic signatures
Functional gene set signatures are also a useful point of comparison between species
Subsetting functions into associated Biological Domains allows for more granular comparisons.