Mouse-human alignment of transcriptomic signatures
Overview
Teaching: 30 min
Exercises: 10 minQuestions
How well transcriptomic changes we observe in mouse models carrying AD-related mutations align with human AD data?
How do we perfrom corss-species comparison
Objectives
Understand the human AD modules.
Approach to align mouse data to human data
Perform correlation analysis.
visualize the results
Author: Ravi Pandey, Jackson Laboratory
Aligning Human and Mouse Phenotype
ALZHEIMER’S DISEASE (AD) is complex disease, we do not expect these mouse models have complete LOAD (late-onset AD) pathology. We can do MRI as well PET imaging to match back to human imaging study ADNI, we can do neuropathology, finally we can do lots of Genomics, proteomics, and metabolomics. These omics study allows us to do real direct homology comparison between human and mouse as genes are overwhemly shared between these two species.
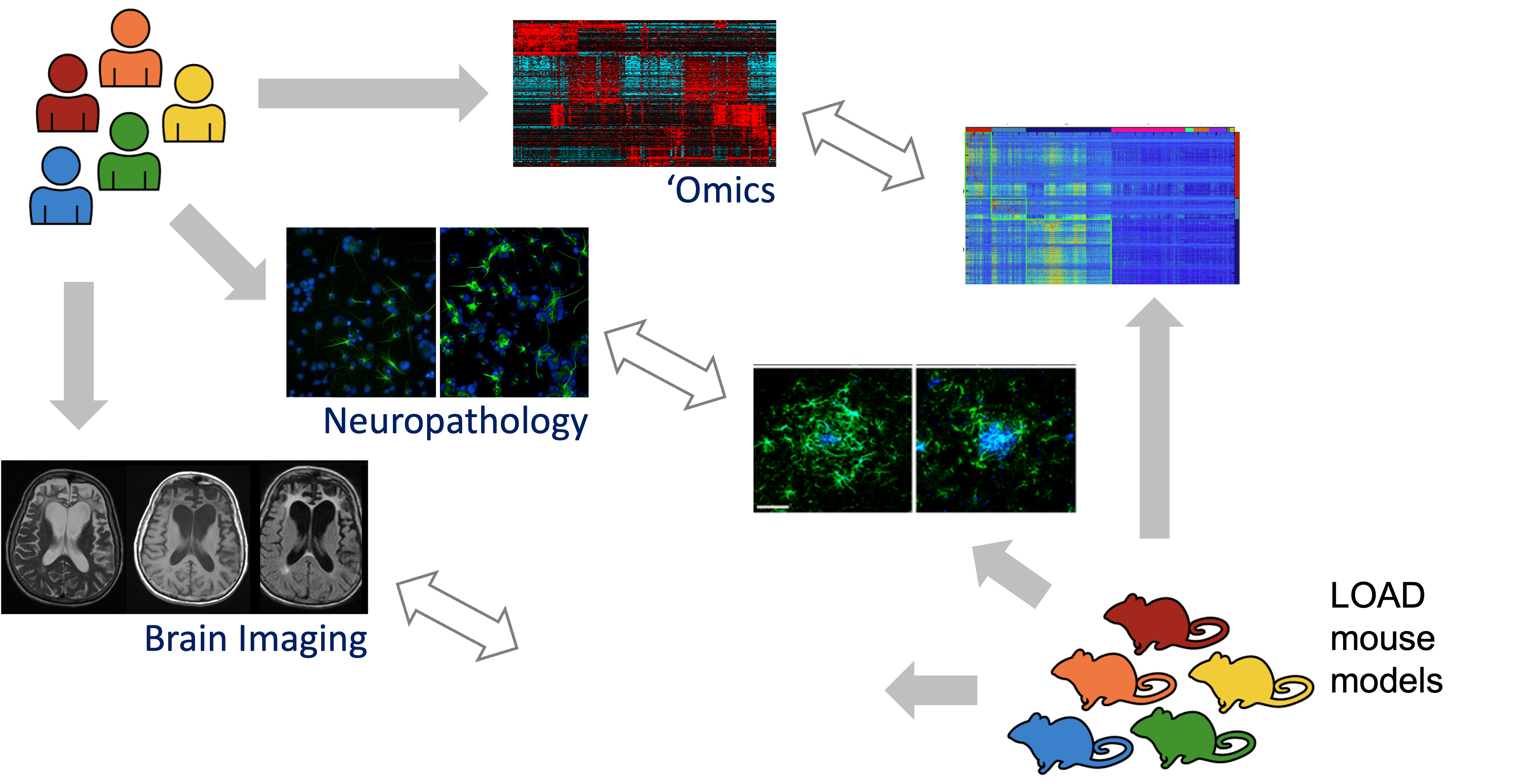
Overview of Human transcriptomic data
Three independent human brain transcriptome studies ROSMAP [Religious Orders Study and the Memory and Aging Project], MSSM [Mount Sinai School of Medicine], and Mayo collected human postmortem brain RNA-seq data from seven distinct regions: dorsolateral prefrontal cortex (DLPFC), temporal cortex (TCX), inferior frontal gyrus (IFG), superior temporal gyrus (STG), frontal pole (FP), parahippocampal gyrus (PHG), and cerebellum (CBE),
These postmortem samples are generally balanced for AD, MCI, and non-effected controls. This really give us broad assessment how AD as affecetd multiple brain region in 3 different population around the US.
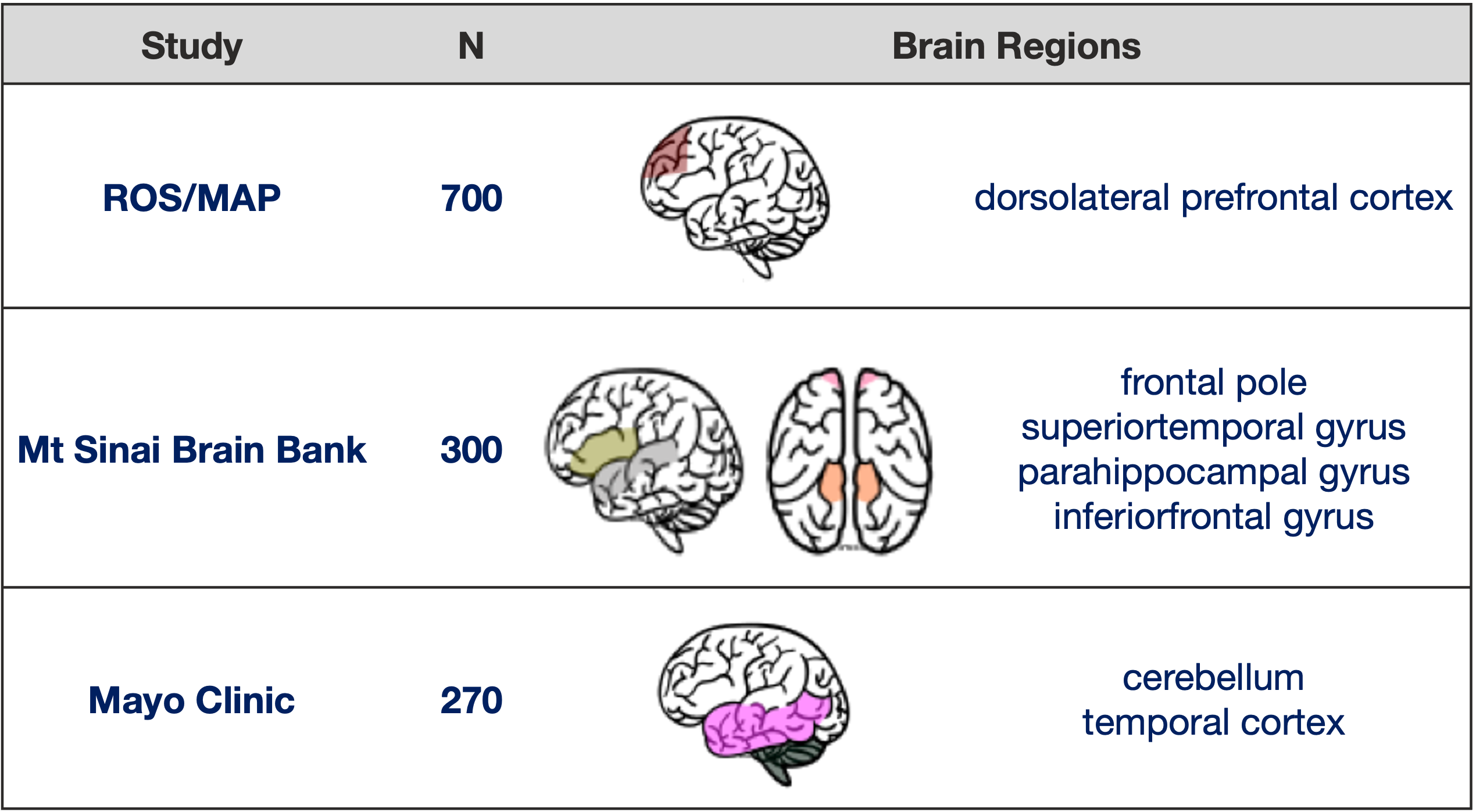
Overview of Human Consensus RNA-Seq Coexpression Modules
The Accelerating Medicines Partnership-Alzheimer’s Disease (AMP-AD) Consortium has generated RNA-seq profiles from more than 1,200 human brains and is applying systems biology approaches toward the goal of elucidating AD mechanisms and potential therapeutic targets.
Wan, et al. performed meta analysis including all available AMP-AD RNA-seq datasets and systematically define correspondences between gene expression changes associated with AD in human brains. Briefly, Wan, et al. performed library normalization and covariate adjustments for each human study separately using fixed/mixed effects modeling to account for batch effects. Among the 2978 AMP-AD modules identified across all tissues, 660 modules were selected which showed an enrichment for at least one AD-specific differential expressed gene set from the meta-analysis in cases compared to controls.
Next, they performed multi method co-expression network analysis followed by differential analysis and found 30 co-expression modules related LOAD pathology from human cohort study. Among the 30 aggregate co-expression modules, five consensus clusters have been described by Wan, et al. These consensus clusters consist of a subset of modules which are associated with similar AD related changes across the multiple studies and brain regions. Further, they looked for enrichment of cell type signature in these modules using expression-weighted cell type enrichment analysis Skene and Grant, 2016 as well as applied functional annotation to these modules.
First module block enriched in astrocytes, next block is enriched in endothelial and microglial genes suggesting strong inflammation component, next block in strongly enriched in neuron suggesting neurodegeneration, next is enriched in oligodendrocytes and glial genes suggesting myelination and finally mixed modules that have things to do like stress response and response to unfolded proteins. Stress response not cell specific,so they may be throughout many cells in brain.
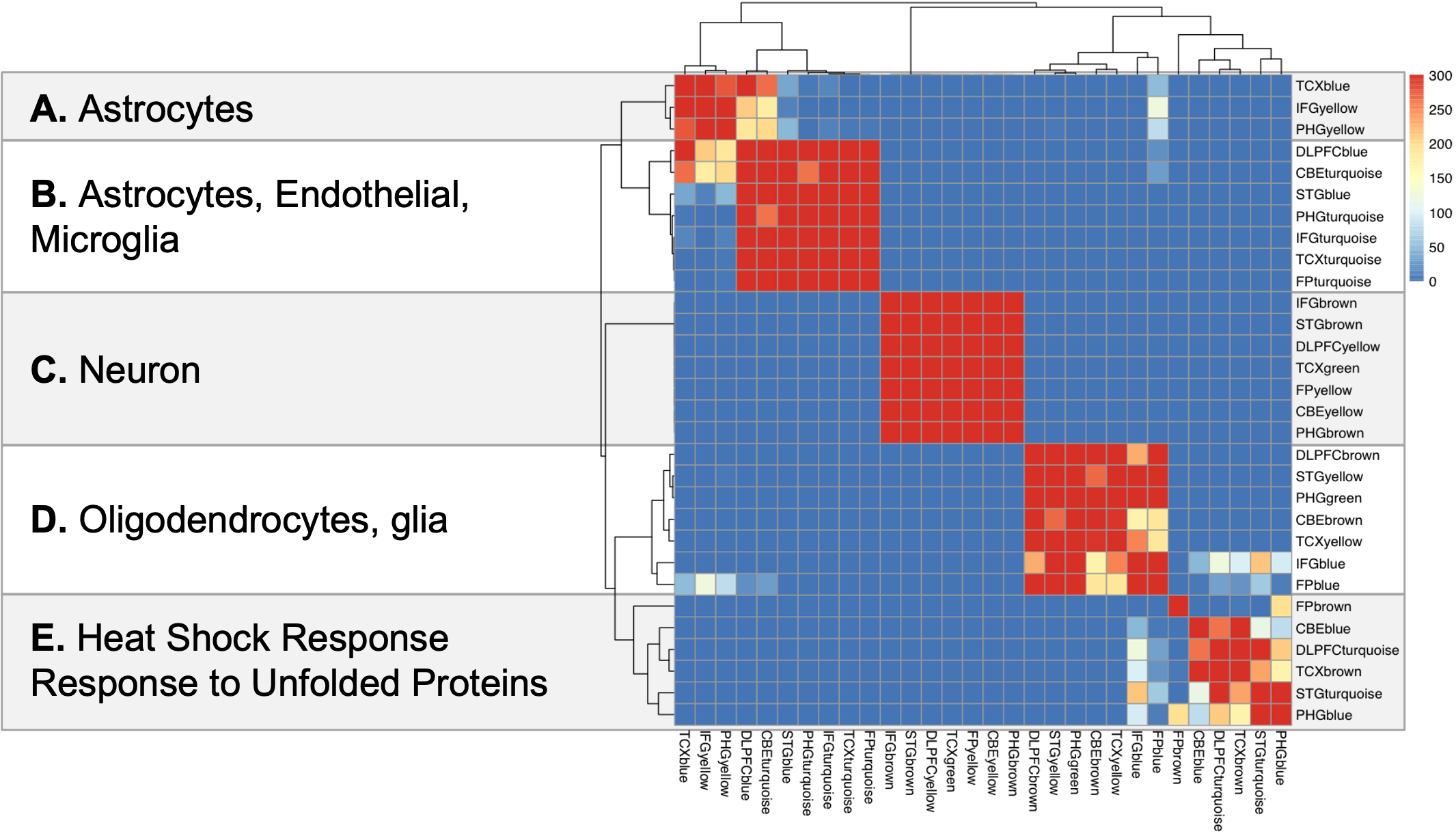
Here we are showing matrix view of gene content overlap between these module, and you can see few strongly overlapping group of modules, implicating similar pathology in different studies in different brain regions.
Reading AMP-AD modules data
You can download data on the 30 human AMP-AD co-expression modules was obtained from the Synapse data repository (https://www.synapse.org/#!Synapse:syn11932957/tables/; SynapseID: syn11932957).
query <- synTableQuery("SELECT * FROM syn11932957")
module_table <- read.table(query$filepath, sep = ",",header = TRUE)
Let’s look at module table
head(module_table)
ROW_ID ROW_VERSION GeneID Module method
1 0 0 ENSG00000168439 DLPFCturquoise aggregate
2 1 0 ENSG00000086061 DLPFCturquoise aggregate
3 2 0 ENSG00000204389 DLPFCturquoise aggregate
4 3 0 ENSG00000114416 DLPFCturquoise aggregate
5 4 0 ENSG00000110172 DLPFCturquoise aggregate
6 5 0 ENSG00000099622 DLPFCturquoise aggregate
ModuleName brainRegion ModuleNameFull
1 aggregateDLPFCturquoise DLPFC aggregateDLPFCturquoiseDLPFC
2 aggregateDLPFCturquoise DLPFC aggregateDLPFCturquoiseDLPFC
3 aggregateDLPFCturquoise DLPFC aggregateDLPFCturquoiseDLPFC
4 aggregateDLPFCturquoise DLPFC aggregateDLPFCturquoiseDLPFC
5 aggregateDLPFCturquoise DLPFC aggregateDLPFCturquoiseDLPFC
6 aggregateDLPFCturquoise DLPFC aggregateDLPFCturquoiseDLPFC
external_gene_name
1 STIP1
2 DNAJA1
3 HSPA1A
4 FXR1
5 CHORDC1
6 CIRBP
Here you see total 9 columns in this table. Column of our interest are: *Colum 2: human ensembl gene ID, *column 3: module name in which gene is clustered and *column 7: is brain tissue. *column 9: is gene names.
How many distinct modules are in table?
length(unique(module_table$Module))
[1] 30
What are the name of modules?
unique(module_table$Module)
[1] "DLPFCturquoise" "DLPFCblue" "DLPFCbrown" "DLPFCyellow"
[5] "CBEturquoise" "CBEblue" "CBEbrown" "CBEyellow"
[9] "TCXturquoise" "TCXblue" "TCXbrown" "TCXyellow"
[13] "TCXgreen" "IFGturquoise" "IFGblue" "IFGbrown"
[17] "IFGyellow" "STGturquoise" "STGblue" "STGbrown"
[21] "STGyellow" "PHGturquoise" "PHGblue" "PHGbrown"
[25] "PHGyellow" "PHGgreen" "FPturquoise" "FPblue"
[29] "FPbrown" "FPyellow"
and how many genes are in each module?
table(module_table$Module)
CBEblue CBEbrown CBEturquoise CBEyellow DLPFCblue
4509 504 1977 1739 1751
DLPFCbrown DLPFCturquoise DLPFCyellow FPblue FPbrown
882 2489 3019 1991 1289
FPturquoise FPyellow IFGblue IFGbrown IFGturquoise
1001 4426 2885 4673 1456
IFGyellow PHGblue PHGbrown PHGgreen PHGturquoise
743 3733 2123 1151 1195
PHGyellow STGblue STGbrown STGturquoise STGyellow
910 1171 3414 2404 1799
TCXblue TCXbrown TCXgreen TCXturquoise TCXyellow
1713 1851 2766 1131 2013
You can also visualize this as bar plot using ggplot2 package.
ggplot(module_table,aes(x=Module)) +
geom_bar() +
theme_bw() +
theme(axis.text.x = ggplot2::element_text(angle = 90, hjust = 0, size = 12))
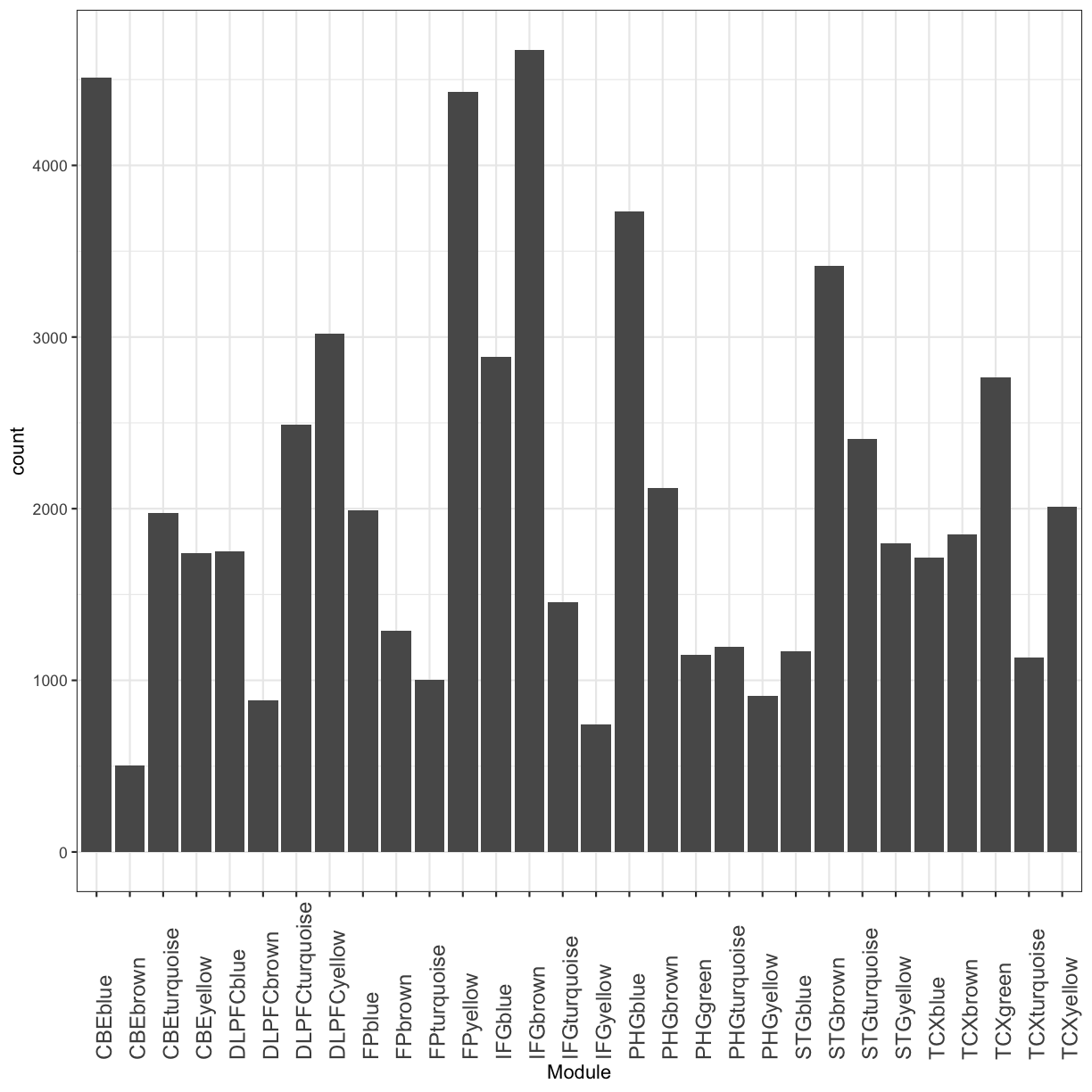
plot of chunk module_nGenes
Challenge 1
What are other ways to count genes in each module?
Solution to Challenge 1
dplyr::count(module_table ,Module)
We can also check total unique genes in table
length(unique((module_table$GeneID)))
[1] 17033
You can also check which modules come from which brain region.
unique(module_table[c("Module", "brainRegion")])
Module brainRegion
1 DLPFCturquoise DLPFC
2490 DLPFCblue DLPFC
4241 DLPFCbrown DLPFC
5123 DLPFCyellow DLPFC
8142 CBEturquoise CBE
10119 CBEblue CBE
14628 CBEbrown CBE
15132 CBEyellow CBE
16871 TCXturquoise TCX
18002 TCXblue TCX
19715 TCXbrown TCX
21566 TCXyellow TCX
23579 TCXgreen TCX
26345 IFGturquoise IFG
27801 IFGblue IFG
30686 IFGbrown IFG
35359 IFGyellow IFG
36102 STGturquoise STG
38506 STGblue STG
39677 STGbrown STG
43091 STGyellow STG
44890 PHGturquoise PHG
46085 PHGblue PHG
49818 PHGbrown PHG
51941 PHGyellow PHG
52851 PHGgreen PHG
54002 FPturquoise FP
55003 FPblue FP
56994 FPbrown FP
58283 FPyellow FP
Mouse-Human orthologous gene conversion
In module table, we have human ENSEMBL ids and gene names. But we will need corresponding mouse gene name, so that we can compare with our results from mouse models. To do this, we are going to add mouse orthologous gene names corresponding to human ENSEMBL id. Mouse orthologs for human genes were extracted using the HCOP tool (The HGNC Comparison of Orthology Predictions) by Wan, et al.. We are going to read that table from the Synapse data repository (https://doi.org/10.7303/syn17010253.1,synapse id:syn17010253)
mouse.human.ortho <- fread(synapser::synGet("syn17010253")$path,check.names = F,header=T)
Let’s see top rows of this ortholog table:
head(mouse.human.ortho)
human_entrez_gene human_ensembl_gene hgnc_id
1: - ENSG00000274059 -
2: - ENSG00000212595 -
3: - ENSG00000277418 -
4: - ENSG00000274759 -
5: - ENSG00000274663 -
6: - ENSG00000277488 -
human_name human_symbol human_chr
1: 5S ribosomal RNA [Source:RFAM;Acc:RF00001] 5S_rRNA 1
2: 5S ribosomal RNA [Source:RFAM;Acc:RF00001] 5S_rRNA X
3: 5S ribosomal RNA [Source:RFAM;Acc:RF00001] 5S_rRNA 8
4: 5S ribosomal RNA [Source:RFAM;Acc:RF00001] 5S_rRNA 4
5: 5S ribosomal RNA [Source:RFAM;Acc:RF00001] 5S_rRNA 17
6: 5S ribosomal RNA [Source:RFAM;Acc:RF00001] 5S_rRNA 17
human_assert_ids mouse_entrez_gene mouse_ensembl_gene mgi_id
1: ENSG00000274059 - ENSMUSG00000089601 MGI:5451871
2: ENSG00000212595 - ENSMUSG00000088132 MGI:5452363
3: ENSG00000277418 - ENSMUSG00000088814 MGI:5452162
4: ENSG00000274759 - ENSMUSG00000084431 MGI:4421893
5: ENSG00000274663 - ENSMUSG00000084588 MGI:4421913
6: ENSG00000277488 - ENSMUSG00000084588 MGI:4421913
mouse_name mouse_symbol mouse_chr mouse_assert_ids support
1: predicted gene, 22094 Gm22094 - ENSMUSG00000089601 Ensembl
2: predicted gene, 22586 Gm22586 - ENSMUSG00000088132 Ensembl
3: predicted gene, 22385 Gm22385 - ENSMUSG00000088814 Ensembl
4: nuclear encoded rRNA 5S 48 n-R5s48 - ENSMUSG00000084431 Ensembl
5: nuclear encoded rRNA 5S 68 n-R5s68 - ENSMUSG00000084588 Ensembl
6: nuclear encoded rRNA 5S 68 n-R5s68 - ENSMUSG00000084588 Ensembl
Add mouse gene names from ortholog table to module table by matching human ENSEMBL ids from both tables .
module_table$Mouse_gene_name <- mouse.human.ortho$mouse_symbol[match(module_table$GeneID,mouse.human.ortho$human_ensembl_gene)]
head(module_table)
ROW_ID ROW_VERSION GeneID Module method
1 0 0 ENSG00000168439 DLPFCturquoise aggregate
2 1 0 ENSG00000086061 DLPFCturquoise aggregate
3 2 0 ENSG00000204389 DLPFCturquoise aggregate
4 3 0 ENSG00000114416 DLPFCturquoise aggregate
5 4 0 ENSG00000110172 DLPFCturquoise aggregate
6 5 0 ENSG00000099622 DLPFCturquoise aggregate
ModuleName brainRegion ModuleNameFull
1 aggregateDLPFCturquoise DLPFC aggregateDLPFCturquoiseDLPFC
2 aggregateDLPFCturquoise DLPFC aggregateDLPFCturquoiseDLPFC
3 aggregateDLPFCturquoise DLPFC aggregateDLPFCturquoiseDLPFC
4 aggregateDLPFCturquoise DLPFC aggregateDLPFCturquoiseDLPFC
5 aggregateDLPFCturquoise DLPFC aggregateDLPFCturquoiseDLPFC
6 aggregateDLPFCturquoise DLPFC aggregateDLPFCturquoiseDLPFC
external_gene_name Mouse_gene_name
1 STIP1 Stip1
2 DNAJA1 Dnaja1
3 HSPA1A Hspa1a
4 FXR1 Fxr1
5 CHORDC1 Chordc1
6 CIRBP Cirbp
We will only keep column of our interest and non-empty entries:
ampad_modules <- module_table %>%
distinct(tissue = brainRegion, module = Module, gene = GeneID, Mouse_gene_name) %>%
filter(Mouse_gene_name != "")
head(ampad_modules)
tissue module gene Mouse_gene_name
1 DLPFC DLPFCturquoise ENSG00000168439 Stip1
2 DLPFC DLPFCturquoise ENSG00000086061 Dnaja1
3 DLPFC DLPFCturquoise ENSG00000204389 Hspa1a
4 DLPFC DLPFCturquoise ENSG00000114416 Fxr1
5 DLPFC DLPFCturquoise ENSG00000110172 Chordc1
6 DLPFC DLPFCturquoise ENSG00000099622 Cirbp
Reading differential expression result of human data from meta-analysis
Differential expression meta-analysis of reprocessed RNASeq data from AMP-AD (all 7 brain regions). LogFC values for human transcripts were obtained via the AMP-AD knowledge portal(https://www.synapse.org/#!Synapse:syn11180450; SynapseID: syn11180450).
ampad_modules_raw <- fread(synapser::synGet("syn11180450")$path,check.names = F,header=T)
Let’s check the data
head(ampad_modules_raw)
Model Tissue Comparison ensembl_gene_id logFC CI.L
1: SourceDiagnosis CBE AD-CONTROL ENSG00000078043 -0.4455482 -0.5474320
2: SourceDiagnosis CBE AD-CONTROL ENSG00000205302 0.4534512 0.3452585
3: SourceDiagnosis CBE AD-CONTROL ENSG00000134982 0.5778206 0.4383669
4: SourceDiagnosis CBE AD-CONTROL ENSG00000173230 0.5924321 0.4493164
5: SourceDiagnosis CBE AD-CONTROL ENSG00000115204 -0.3426223 -0.4257147
6: SourceDiagnosis CBE AD-CONTROL ENSG00000163867 -0.3176858 -0.3965217
CI.R AveExpr t P.Value adj.P.Val B Direction
1: -0.3436645 1.3320969 -8.592843 1.206969e-16 2.053175e-12 27.12967 DOWN
2: 0.5616439 2.9361993 8.235175 1.699316e-15 1.445353e-11 24.54943 UP
3: 0.7172742 3.5498628 8.141480 3.365041e-15 1.530863e-11 23.85060 UP
4: 0.7355477 3.0759381 8.133894 3.599700e-15 1.530863e-11 23.81776 UP
5: -0.2595299 2.2634337 -8.102128 4.512223e-15 1.535148e-11 23.62730 DOWN
6: -0.2388499 0.4404036 -7.918097 1.695179e-14 4.806115e-11 22.34035 DOWN
hgnc_symbol percentage_gc_content gene.length Sex Study
1: PIAS2 38.59 17527 ALL MAYO
2: SNX2 36.08 4254 ALL MAYO
3: APC 37.63 12440 ALL MAYO
4: GOLGB1 38.07 11865 ALL MAYO
5: MPV17 50.33 5625 ALL MAYO
6: ZMYM6 38.80 9591 ALL MAYO
Data came from how many tissues?
unique(ampad_modules_raw$Tissue)
[1] "CBE" "TCX" "FP" "IFG" "PHG" "STG" "DLPFC"
We see that data is from all 7 brain regions.
AMP-AD data has been processed many ways and using different models and comparisons. Let’s see how many ways data has been analyzed,
unique(ampad_modules_raw$Comparison)
[1] "AD-CONTROL" "PATH_AGE-CONTROL"
[3] "PSP-CONTROL" "AD-PATH_AGE"
[5] "AD-OTHER" "OTHER-CONTROL"
[7] "2-0" "2-1"
[9] "1-0" "CDR"
[11] "4-1" "4-2"
[13] "FEMALE-MALE" "AD-CONTROL.IN.FEMALE-MALE"
[15] "AOD"
For our analysis, we need data for “Diagnosis” model and comparison between cases vs controls. So, we subset the logFC data for these conditions. Also, we need only three columns: “Tissue”,”Gene” and “logFC”. So, we will filter and subset the data.
ampad_fc <- ampad_modules_raw %>%
as_tibble() %>%
filter(Model == "Diagnosis", Comparison == "AD-CONTROL") %>%
dplyr::select(tissue = Tissue, gene = ensembl_gene_id, ampad_fc = logFC)
Combine with modules so correlation can be done per module
Next, we will combine fold change table ampad_fc and module table ampad_modules. First, look at both tables to check how can we merge them together?
head(ampad_fc)
# A tibble: 6 × 3
tissue gene ampad_fc
<chr> <chr> <dbl>
1 CBE ENSG00000085224 0.363
2 CBE ENSG00000131016 0.481
3 CBE ENSG00000078043 -0.361
4 CBE ENSG00000243943 -0.257
5 CBE ENSG00000093167 -0.477
6 CBE ENSG00000058272 0.330
head(ampad_modules)
tissue module gene Mouse_gene_name
1 DLPFC DLPFCturquoise ENSG00000168439 Stip1
2 DLPFC DLPFCturquoise ENSG00000086061 Dnaja1
3 DLPFC DLPFCturquoise ENSG00000204389 Hspa1a
4 DLPFC DLPFCturquoise ENSG00000114416 Fxr1
5 DLPFC DLPFCturquoise ENSG00000110172 Chordc1
6 DLPFC DLPFCturquoise ENSG00000099622 Cirbp
In both tables, common columns are “gene” and “tissue”. So we will merge both datasets using these two columns. Reminder: Every gene can be present in multiple brain regions but only one module form any brain region. Let’s check that:
ampad_modules[ampad_modules$gene %in% "ENSG00000168439",]
tissue module gene Mouse_gene_name
1 DLPFC DLPFCturquoise ENSG00000168439 Stip1
9376 CBE CBEblue ENSG00000168439 Stip1
17627 TCX TCXbrown ENSG00000168439 Stip1
31448 STG STGturquoise ENSG00000168439 Stip1
40130 PHG PHGblue ENSG00000168439 Stip1
48317 FP FPblue ENSG00000168439 Stip1
We can see that this gene is present in six distinct modules and all modules are from different brain regions. You can do for any other gene as well.
Let’s merge using inner_join function from tidyverse:
ampad_modules_fc <- ampad_modules %>%
inner_join(ampad_fc, by = c("gene", "tissue")) %>%
dplyr::select(symbol = Mouse_gene_name, module, ampad_fc)
head(ampad_modules_fc)
symbol module ampad_fc
1 Stip1 DLPFCturquoise 0.03342379
2 Dnaja1 DLPFCturquoise 0.02350154
3 Hspa1a DLPFCturquoise 0.10220020
4 Fxr1 DLPFCturquoise 0.03842087
5 Chordc1 DLPFCturquoise 0.06350503
6 Cirbp DLPFCturquoise -0.24214640
We will use ampad_modules_fc dataset to compare with log fold change data from mouse models.
Preparing module information for correlation plot
mod <- c("TCXblue","PHGyellow","IFGyellow","DLPFCblue","CBEturquoise","STGblue","PHGturquoise","IFGturquoise","TCXturquoise","FPturquoise","IFGbrown","STGbrown","DLPFCyellow","TCXgreen","FPyellow","CBEyellow","PHGbrown","DLPFCbrown","STGyellow","PHGgreen","CBEbrown","TCXyellow","IFGblue","FPblue","FPbrown","CBEblue","DLPFCturquoise","TCXbrown","STGturquoise","PHGblue")
cluster_a <- tibble(
module = c("TCXblue", "PHGyellow", "IFGyellow"),
cluster = "Consensus Cluster A (ECM organization)",
cluster_label = "Consensus Cluster A\n(ECM organization)"
)
cluster_b <- tibble(
module = c("DLPFCblue", "CBEturquoise", "STGblue", "PHGturquoise", "IFGturquoise", "TCXturquoise", "FPturquoise"),
cluster = "Consensus Cluster B (Immune system)",
cluster_label = "Consensus Cluster B\n(Immune system)"
)
cluster_c <- tibble(
module = c("IFGbrown", "STGbrown", "DLPFCyellow", "TCXgreen", "FPyellow", "CBEyellow", "PHGbrown"),
cluster = "Consensus Cluster C (Neuronal system)",
cluster_label = "Consensus Cluster C\n(Neuronal system)"
)
cluster_d <- tibble(
module = c("DLPFCbrown", "STGyellow", "PHGgreen", "CBEbrown", "TCXyellow", "IFGblue", "FPblue"),
cluster = "Consensus Cluster D (Cell Cycle, NMD)",
cluster_label = "Consensus Cluster D\n(Cell Cycle, NMD)"
)
cluster_e <- tibble(
module = c("FPbrown", "CBEblue", "DLPFCturquoise", "TCXbrown", "STGturquoise", "PHGblue"),
cluster = "Consensus Cluster E (Organelle Biogensis, Cellular stress response)",
cluster_label = "Consensus Cluster E\n(Organelle Biogenesis,\nCellular stress response)"
)
module_clusters <- cluster_a %>%
bind_rows(cluster_b) %>%
bind_rows(cluster_c) %>%
bind_rows(cluster_d) %>%
bind_rows(cluster_e) %>%
mutate(cluster_label = fct_inorder(cluster_label))
head(module_clusters)
# A tibble: 6 × 3
module cluster cluster_label
<chr> <chr> <fct>
1 TCXblue Consensus Cluster A (ECM organization) "Consensus Cluster A\n(EC…
2 PHGyellow Consensus Cluster A (ECM organization) "Consensus Cluster A\n(EC…
3 IFGyellow Consensus Cluster A (ECM organization) "Consensus Cluster A\n(EC…
4 DLPFCblue Consensus Cluster B (Immune system) "Consensus Cluster B\n(Im…
5 CBEturquoise Consensus Cluster B (Immune system) "Consensus Cluster B\n(Im…
6 STGblue Consensus Cluster B (Immune system) "Consensus Cluster B\n(Im…
save(ampad_modules_fc,module_clusters,mod,file="../data/AMPADModuleData_Correlation.RData")
Correlation between mouse models and human AD modules
There are two approaches that we adopted to compute correlation between mouse data with human AD modules:
- Compare change in expression in Human AD cases with change in expression in mouse models for each orthologous gene in a given module
- LogFC(h) = log fold change in transcript expression of human AD patients compared to control patients.
- LogFC(m) = log fold change in transcript expression of mouse AD models compare to control mouse models. \(cor.test(LogFC(h), LogFC(m))\)
- Compare Human AD to mouse genetic effects for each orthologous gene in a given module
- h = human gene expression (Log2 RNA-seq Fold Change control/AD)
- β = mouse gene expression effect from linear regression model (Log2 RNA-seq TPM) \(cor.test(LogFC(h), β)\)
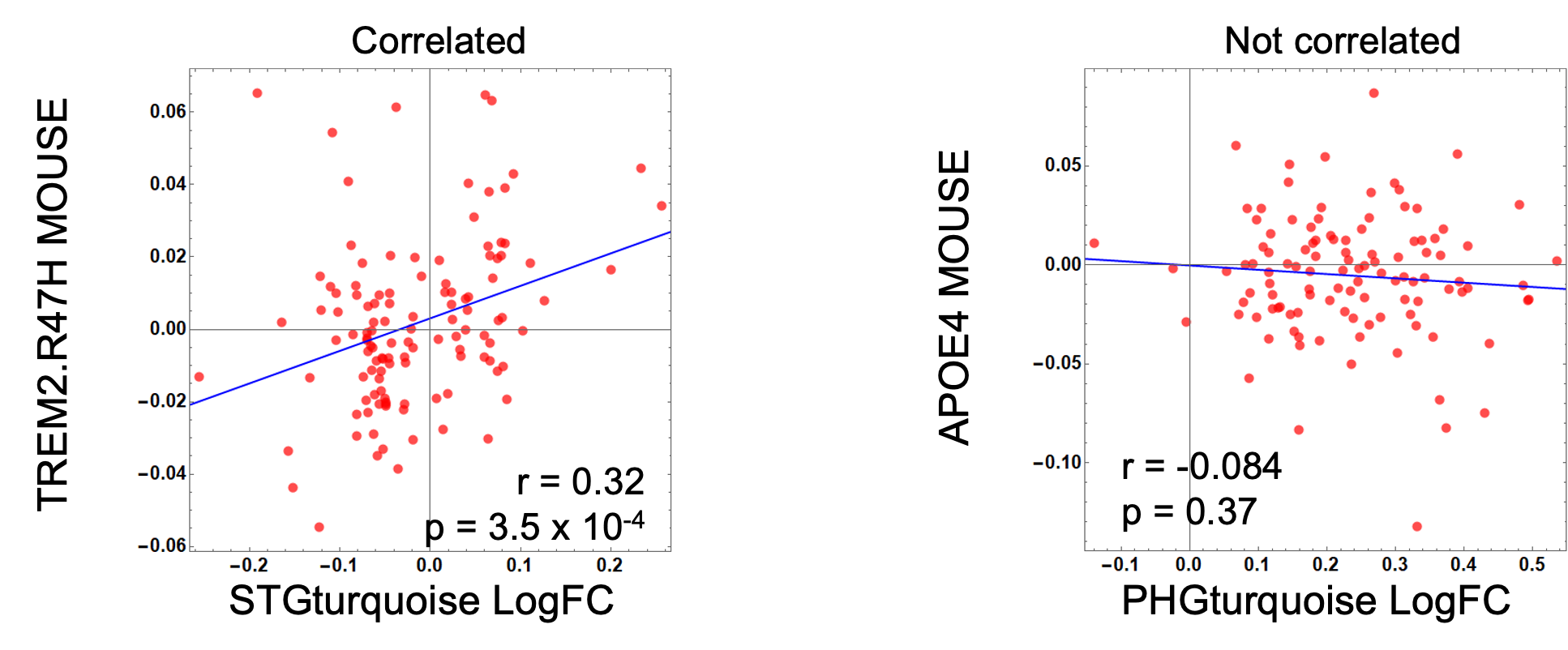
These appraoches allow us to assess directional coherence between AMP-AD modules and the effects of genetic perturbations in mice. In this lesson, we are going to use first approach. Let’s start!
Step0: Reading Gene Expression Count matrix from Previous Lesson
We first read the result table saved after differential analysis in last lesson. We start with 5XFAD mouse model to understand all required steps to perform correlation with human AD modules.
load("../results/DEAnalysis_5XFAD.Rdata")
We can also load AMP-AD module data.
load("../data/AMPADModuleData_Correlation.RData")
Step1: Measure the correlation between mouse models for each sex at each age and AMP-AD modules using common genes from both datasets
We compute pearson correlation between changes in expression for each gene in a given module (log fold change for cases minus controls) with each mouse model (log fold change of the 5XFAD mice minus sex and age-matched B6 mice).
First, we add both mouse DE_5xFAD.df and human ampad_modules_fc log fold change datasets for all genes.
model_vs_ampad <- DE_5xFAD.df %>%
inner_join(ampad_modules_fc, by = c("symbol"),multiple = "all")
head(model_vs_ampad)
symbol EntrezGene baseMean log2FoldChange lfcSE stat pvalue
1 Gnai3 14679 3707.5316 -0.02308587 0.0381646 -0.6049026 0.5452437
2 Gnai3 14679 3707.5316 -0.02308587 0.0381646 -0.6049026 0.5452437
3 Gnai3 14679 3707.5316 -0.02308587 0.0381646 -0.6049026 0.5452437
4 Gnai3 14679 3707.5316 -0.02308587 0.0381646 -0.6049026 0.5452437
5 Scml2 107815 126.8241 0.08939456 0.1377406 0.6490066 0.5163341
6 Scml2 107815 126.8241 0.08939456 0.1377406 0.6490066 0.5163341
padj model sex age module ampad_fc
1 0.9999518 5xFAD male 4 mo TCXblue 0.18017910
2 0.9999518 5xFAD male 4 mo IFGturquoise -0.01064322
3 0.9999518 5xFAD male 4 mo STGblue -0.01063594
4 0.9999518 5xFAD male 4 mo FPturquoise -0.03142185
5 0.9999518 5xFAD male 4 mo STGturquoise 0.07891395
6 0.9999518 5xFAD male 4 mo PHGblue 0.09451007
Next, we create a list-columns of data frame using nest function of tidyverse package. Nesting is implicitly a summarising operation: you get one row for each group defined by the non-nested columns.
df <- model_vs_ampad %>%
dplyr::select(module, model, sex, age, symbol, log2FoldChange, ampad_fc) %>%
group_by(module, model, sex,age) %>%
nest(data = c(symbol, log2FoldChange, ampad_fc))
head(df)
# A tibble: 6 × 5
# Groups: module, model, sex, age [6]
module model sex age data
<chr> <chr> <chr> <chr> <list>
1 TCXblue 5xFAD male 4 mo <tibble [1,462 × 3]>
2 IFGturquoise 5xFAD male 4 mo <tibble [1,310 × 3]>
3 STGblue 5xFAD male 4 mo <tibble [1,092 × 3]>
4 FPturquoise 5xFAD male 4 mo <tibble [927 × 3]>
5 STGturquoise 5xFAD male 4 mo <tibble [1,748 × 3]>
6 PHGblue 5xFAD male 4 mo <tibble [2,841 × 3]>
total number of groups in data table
dim(df)
[1] 180 5
Let’s check first row:
head(df[1,]$data)
[[1]]
# A tibble: 1,462 × 3
symbol log2FoldChange ampad_fc
<chr> <dbl> <dbl>
1 Gnai3 -0.0231 0.180
2 Gna12 -0.00445 0.444
3 Sdhd -0.00152 0.0631
4 Lhx2 -0.0959 0.252
5 Gmpr 0.0105 0.801
6 Tpd52l1 -0.103 0.714
7 Cdh4 -0.0111 0.109
8 Dbt -0.0460 -0.0103
9 Tbrg4 0.00746 -0.129
10 Galnt1 -0.0105 0.191
# ℹ 1,452 more rows
Next, we compute correlation coefficients using cor.test function built in R as following:
cor.df <- df %>%
mutate(
cor_test = map(data, ~ cor.test(.x[["log2FoldChange"]], .x[["ampad_fc"]], method = "pearson")),
estimate = map_dbl(cor_test, "estimate"),
p_value = map_dbl(cor_test, "p.value")
) %>%
ungroup() %>%
dplyr::select(-cor_test)
head(cor.df)
# A tibble: 6 × 7
module model sex age data estimate p_value
<chr> <chr> <chr> <chr> <list> <dbl> <dbl>
1 TCXblue 5xFAD male 4 mo <tibble [1,462 × 3]> 0.0681 9.19e- 3
2 IFGturquoise 5xFAD male 4 mo <tibble [1,310 × 3]> 0.227 9.10e-17
3 STGblue 5xFAD male 4 mo <tibble [1,092 × 3]> 0.284 9.55e-22
4 FPturquoise 5xFAD male 4 mo <tibble [927 × 3]> 0.103 1.72e- 3
5 STGturquoise 5xFAD male 4 mo <tibble [1,748 × 3]> -0.0538 2.44e- 2
6 PHGblue 5xFAD male 4 mo <tibble [2,841 × 3]> -0.00934 6.19e- 1
Step2: add signifcant correlations and join module cluster information to correlation table
model_module <- cor.df %>%
mutate(significant = p_value < 0.05) %>%
left_join(module_clusters, by = "module") %>%
dplyr::select(cluster, cluster_label, module, model, sex,age,correlation = estimate, p_value, significant)
head(model_module)
# A tibble: 6 × 9
cluster cluster_label module model sex age correlation p_value
<chr> <fct> <chr> <chr> <chr> <chr> <dbl> <dbl>
1 Consensus Cluster… "Consensus C… TCXbl… 5xFAD male 4 mo 0.0681 9.19e- 3
2 Consensus Cluster… "Consensus C… IFGtu… 5xFAD male 4 mo 0.227 9.10e-17
3 Consensus Cluster… "Consensus C… STGbl… 5xFAD male 4 mo 0.284 9.55e-22
4 Consensus Cluster… "Consensus C… FPtur… 5xFAD male 4 mo 0.103 1.72e- 3
5 Consensus Cluster… "Consensus C… STGtu… 5xFAD male 4 mo -0.0538 2.44e- 2
6 Consensus Cluster… "Consensus C… PHGbl… 5xFAD male 4 mo -0.00934 6.19e- 1
# ℹ 1 more variable: significant <lgl>
Step3: Create a dataframe to use as input for plotting the results
order.model <- c("5xFAD (Male)", "5xFAD (Female)")
correlation_for_plot <- model_module %>%
arrange(cluster) %>%
mutate(
module = factor(module,levels=mod),
model_sex = glue::glue("{model} ({str_to_title(sex)})"),
) %>%
arrange(model_sex) %>%
mutate(
model_sex = factor(model_sex,levels=order.model),
model_sex = fct_rev(model_sex),
)
head(correlation_for_plot)
# A tibble: 6 × 10
cluster cluster_label module model sex age correlation p_value significant
<chr> <fct> <fct> <chr> <chr> <chr> <dbl> <dbl> <lgl>
1 Consen… "Consensus C… TCXbl… 5xFAD fema… 4 mo 0.114 1.31e-5 TRUE
2 Consen… "Consensus C… PHGye… 5xFAD fema… 4 mo 0.201 9.14e-9 TRUE
3 Consen… "Consensus C… IFGye… 5xFAD fema… 4 mo 0.0757 5.12e-2 FALSE
4 Consen… "Consensus C… TCXbl… 5xFAD fema… 6 mo 0.115 9.69e-6 TRUE
5 Consen… "Consensus C… PHGye… 5xFAD fema… 6 mo 0.0668 5.87e-2 FALSE
6 Consen… "Consensus C… IFGye… 5xFAD fema… 6 mo 0.0707 6.86e-2 FALSE
# ℹ 1 more variable: model_sex <fct>
Visualizing the Correlation plot
Now, we will use above matrix and visualize the correlation results using ggplot2 package.
data <- correlation_for_plot
range(correlation_for_plot$correlation)
[1] -0.1749441 0.3684976
ggplot2::ggplot() +
ggplot2::geom_tile(data = data, ggplot2::aes(x = .data$module, y = .data$model_sex), colour = "black", fill = "white") +
ggplot2::geom_point(data = dplyr::filter(data), ggplot2::aes(x = .data$module, y = .data$model_sex, colour = .data$correlation, size = abs(.data$correlation))) +
ggplot2::geom_point(data = dplyr::filter(data, .data$significant), ggplot2::aes(x = .data$module, y = .data$model_sex, colour = .data$correlation),color="black",shape=0,size=9) +
ggplot2::scale_x_discrete(position = "top") +
ggplot2::scale_size(guide = "none", limits = c(0, 0.4)) +
ggplot2::scale_color_gradient2(limits = c(-0.4, 0.4), breaks = c(-0.4, 0, 0.4), low = "#85070C", high = "#164B6E", name = "Correlation", guide = ggplot2::guide_colorbar(ticks = FALSE)) +
ggplot2::labs(x = NULL, y = NULL) +
ggplot2::facet_grid( rows = dplyr::vars(.data$age),cols = dplyr::vars(.data$cluster_label), scales = "free", space = "free",switch = 'y') +
ggplot2::theme(
strip.text.x = ggplot2::element_text(size = 10,colour = c("black")),
strip.text.y.left = ggplot2::element_text(angle = 0,size = 12),
axis.ticks = ggplot2::element_blank(),
axis.text.x = ggplot2::element_text(angle = 90, hjust = 0, size = 12),
axis.text.y = ggplot2::element_text(angle = 0, size = 12),
panel.background = ggplot2::element_blank(),
plot.title = ggplot2::element_text(angle = 0, vjust = -54, hjust = 0.03,size=12,face="bold"),
plot.title.position = "plot",
panel.grid = ggplot2::element_blank(),
legend.position = "right"
)

In above plot, top row represent 30 AMP-AD modules grouped into 5 consensus clusters describing the major functional groups of AD-related alterations and left column represent mouse models. Positive correlations are shown in blue and negative correlations in red. Color intensity and size of the circles are proportional to the correlation coefficient. Black square around dots represent significant correlation at p-value=0.05 and non-significant correlations are left blank.
Male and female 5XFAD mice display gene expression alterations across all five consensus clusters, with the most pronounced alterations observed in Consensus Cluster B, which consists of immune system pathways.
We also saw in Volcano plot that immune-related genes were signifcantly overexpressed in the 5XFAD model. This significant positive correlation suggest that 5XFAD model capture inflammatory changes observed in human AD patients.
Combing all steps into a function to perform correlation analysis
We can combine all above steps to perform correlation analysis into one function to use for other data by just inputting log fod change matrix obtained from differential analysis.
corr_function <- function(mydat)
{
model_vs_ampad <- mydat %>%
inner_join(ampad_modules_fc, by = c("symbol"),multiple = "all") %>%
dplyr::select(module, model, sex, age, symbol, log2FoldChange, ampad_fc) %>%
group_by(module, model, sex,age) %>%
nest(data = c(symbol, log2FoldChange, ampad_fc)) %>%
mutate(
cor_test = map(data, ~ cor.test(.x[["log2FoldChange"]], .x[["ampad_fc"]], method = "pearson")),
estimate = map_dbl(cor_test, "estimate"),
p_value = map_dbl(cor_test, "p.value")
) %>%
ungroup() %>%
dplyr::select(-cor_test)
model_module <- model_vs_ampad %>%
mutate(significant = p_value < 0.05) %>%
left_join(module_clusters, by = "module") %>%
dplyr::select(cluster, cluster_label, module, model, sex,age,correlation = estimate, p_value, significant)
correlation_for_plot <- model_module %>%
arrange(cluster) %>%
mutate(
module = factor(module,levels=mod),
model_sex = glue::glue("{model} ({str_to_title(sex)})"),
) %>%
arrange(model_sex) %>%
mutate(
model_sex = factor(model_sex,levels=order.model),
model_sex = fct_rev(model_sex),
)
}
magora_corrplot <- function(data,ran)
{
ggplot2::ggplot() +
ggplot2::geom_tile(data = data, ggplot2::aes(x = .data$module, y = .data$model_sex), colour = "black", fill = "white") +
ggplot2::geom_point(data = dplyr::filter(data), ggplot2::aes(x = .data$module, y = .data$model_sex, colour = .data$correlation, size = abs(.data$correlation))) +
ggplot2::geom_point(data = dplyr::filter(data, .data$significant), ggplot2::aes(x = .data$module, y = .data$model_sex, colour = .data$correlation),color="black",shape=0,size=9) +
ggplot2::scale_x_discrete(position = "top") +
ggplot2::scale_size(guide = "none", limits = c(0, ran)) +
ggplot2::scale_color_gradient2(limits = c(-ran, ran), breaks = c(-ran, 0, ran), low = "#85070C", high = "#164B6E", name = "Correlation", guide = ggplot2::guide_colorbar(ticks = FALSE)) +
ggplot2::labs(x = NULL, y = NULL) +
#ggplot2::ggtitle("Model(Sex)| Age/Control") +
ggplot2::facet_grid( rows = dplyr::vars(.data$age),cols = dplyr::vars(.data$cluster_label), scales = "free", space = "free",switch = 'y') +
ggplot2::theme(
strip.text.x = ggplot2::element_text(size = 10,colour = c("black")),
strip.text.y.left = ggplot2::element_text(angle = 0,size = 12),
axis.ticks = ggplot2::element_blank(),
axis.text.x = ggplot2::element_text(angle = 90, hjust = 0, size = 12),
axis.text.y = ggplot2::element_text(angle = 0, size = 12),
panel.background = ggplot2::element_blank(),
plot.title = ggplot2::element_text(angle = 0, vjust = -54, hjust = 0.03,size=12,face="bold"),
plot.title.position = "plot",
panel.grid = ggplot2::element_blank(),
legend.position = "right"
)
}
We can use these functions directly onto our other dataset from LOAD1 cohort.
Correlation between LOAD1 models and human AD modules
Reading Gene Expression Count matrix of LOAD1 cohort from Previous Lesson
load("../results/DEAnalysis_LOAD1.Rdata")
First, check the data:
head(DE_LOAD1.df)
symbol EntrezGene baseMean log2FoldChange lfcSE
ENSMUSG00000000001 Gnai3 14679 2587.33246 -0.027251874 0.05341582
ENSMUSG00000000028 Cdc45 12544 96.38913 -0.086316094 0.19815501
ENSMUSG00000000031 H19 14955 23.15992 -0.402670365 0.47978365
ENSMUSG00000000037 Scml2 107815 94.24871 -0.093235144 0.23666227
ENSMUSG00000000049 Apoh 11818 11.94380 -0.220259366 0.59500274
ENSMUSG00000000056 Narf 67608 3464.49361 0.009537733 0.05167193
stat pvalue padj model sex age
ENSMUSG00000000001 -0.5101836 0.6099228 0.9968456 APOE4 male 4
ENSMUSG00000000028 -0.4355989 0.6631278 0.9968456 APOE4 male 4
ENSMUSG00000000031 -0.8392749 0.4013151 0.9932419 APOE4 male 4
ENSMUSG00000000037 -0.3939586 0.6936116 0.9968456 APOE4 male 4
ENSMUSG00000000049 -0.3701821 0.7112468 0.9968456 APOE4 male 4
ENSMUSG00000000056 0.1845825 0.8535565 0.9968456 APOE4 male 4
unique(DE_LOAD1.df$model)
[1] "APOE4" "Trem2" "APOE4Trem2"
unique(DE_LOAD1.df$sex)
[1] "male" "female"
unique(DE_LOAD1.df$age)
[1] 4 8 12
Perform the correlation analysis
We directly input logFC table DE_LOAD1.df to corr_function:
order.model <- c("APOE4 (Male)", "APOE4 (Female)","Trem2 (Male)", "Trem2 (Female)","APOE4Trem2 (Male)", "APOE4Trem2 (Female)")
correlation_for_plot <- corr_function(DE_LOAD1.df)
head(correlation_for_plot)
# A tibble: 6 × 10
cluster cluster_label module model sex age correlation p_value significant
<chr> <fct> <fct> <chr> <chr> <int> <dbl> <dbl> <lgl>
1 Consen… "Consensus C… TCXbl… APOE4 fema… 4 -0.0251 3.37e-1 FALSE
2 Consen… "Consensus C… PHGye… APOE4 fema… 4 -0.148 2.34e-5 TRUE
3 Consen… "Consensus C… IFGye… APOE4 fema… 4 0.0911 1.86e-2 TRUE
4 Consen… "Consensus C… TCXbl… APOE4 fema… 8 -0.0230 3.79e-1 FALSE
5 Consen… "Consensus C… PHGye… APOE4 fema… 8 -0.110 1.73e-3 TRUE
6 Consen… "Consensus C… IFGye… APOE4 fema… 8 -0.0566 1.45e-1 FALSE
# ℹ 1 more variable: model_sex <fct>
Visualize the correlation plot
#range of correlation
range(correlation_for_plot$correlation)
[1] -0.2256401 0.1073370
magora_corrplot(correlation_for_plot,0.25)
What do you conclude from this plot?
Key Points
AMP-AD gene modules represent major transcriptomic heterogeneity in AD.
Correlation of logFC is a practical approach for human-mouse alignment of AD-associated transcriptomic signatures.